Surface area of a cube

To derive the formula of the surface area of a cube, you will need to start with a cube as shown below and call the length of one side a.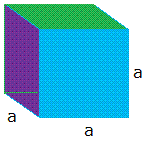


In order to make a cube like the one shown above, you basically need to use the following cube template:



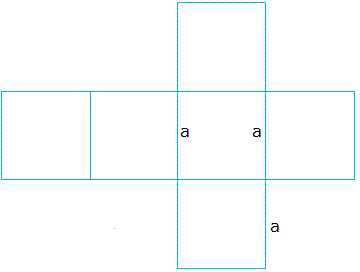
Looking at the cube template, it is easy to see that the cube has six sides and each side is a square.

Since the length of an edge is a, the area of one square is a × a = a²

Since there are six sides, the total surface area, call it SA, can be found as shown below:

SA = a² + a² + a² + a² + a² + a²

SA = 6 × a²

A few examples showing how to find the surface area of a cube

Example #1:

Find the surface area if the length of one side is 3 cm.

Surface area = 6 × a²

Surface area = 6 × 3²

Surface area = 6 × 3 × 3

Surface area = 6 × 9

Surface area = 54 cm²


Example #2:

Find the surface area if the length of one side is 5 cm.

Surface area = 6 × a²

Surface area = 6 × 5²

Surface area = 6 × 5 × 5

Surface area = 6 × 25

Surface area = 150 cm²


Example #3:

Find the surface area if the length of one side is 1/2 cm.

Surface area = 6 × a²

Surface area = 6 × (1/2)²

Surface area = 6 × 1/2 × 1/2

Surface area = 6 × 1/4

Surface area = 6/4 cm²

Surface area = 3/2 cm²

Surface area = 1.5 cm²


Example #4:

Find the surface area if the length of one side is 2 1/3 cm.

First, convert 2 1/3 into a proper fraction.

2 1/3 = (2 × 3 + 1) / 3 = (6 + 1)/3 = 7/3

Surface area = 6 × a²

Surface area = 6 × (7/2)²

Surface area = 6 × 7/2 × 7/2

Surface area = 6 × 49/4

Surface area = 294/4 cm²

Surface area = 73.5 cm²