Survey and intersection of three sets

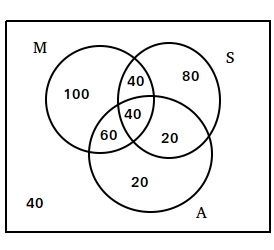
In a survey of 400 students of a college it was found that 240 study mathematics, 180 study statistics and 140 study accounts, 80 study mathematics and statistics, 60 study statistics and accounts, 100 study accounts and mathematics and 40 study none of these subjects. On the
basis of this information answer the following questions.

1) Find the number of students who study at least one of these subjects.
2) Find the number of students who study all of these subjects.

Solution

1) Number of students who study at least one + number of students who study none = total number of students

Number of students who study at least one + 40 = 400

Number of students who study at least one = 400 - 40

Number of students who study at least one = 360

The number of students who study at least one of these subjects is 360.

2)

Let M be the number of students who study math

Let S be the number of students who study statistics

Let A be the number of students who study accounts


Then we need this formula to find the number of students who study all of these subjects.


n(M U S U A) = n(M) + n(S) + n(A) - n(M ∩ S) - n(M ∩ A) - n(S ∩ A) +
n(M ∩ S ∩ A)

360 = 240 + 180 + 140 - 80 - 100 - 60 + n(M ∩ S ∩ A)

360 = 560 - 240 + n(M ∩ S ∩ A)

360 + 240 = 560 + n(M ∩ S ∩ A)

600 = 560 + n(M ∩ S ∩ A)

40 = n(M ∩ S ∩ A)

The number of students who study all of these subjects is 40.