Tangent circles

Tangent circles are coplanar circles that intersect in exactly one point. They can be externally tangent or internally tangent.

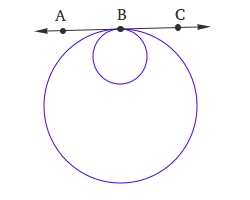
Circles that are tangent internally

Circles that are tangent internally have one circle inside the other. In the image below, you can clearly see that the smaller circle is located inside the bigger circle. Furthermore, both circles share point B as a common point. Therefore, B is the point of tangency.

Line AC is called common tangent because line AC is tangent to both the small circle and the big circle.

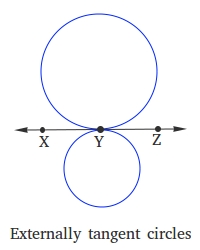
Externally tangent circles

Circles that are tangent externally are completely outside of each other. In the image below, you can see that both circles are completely outside of each other. Furthermore, both circles share point Y as a common point. Therefore, Y is the point of tangency.

Line XZ is called common tangent because line XZ is tangent to both circles.

Relationship between two tangent circles, the centers of the circles, and the radii of the circles.

Using the two circles above that are tangent internally, draw the line between the centers of the circles and passing through the point of tangency B.

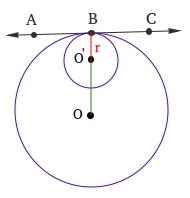
1. Line OB is perpendicular to line AC.

2. The distance between the centers of the two circles (green line) plus the radius of the smaller circle (red line) is equal to the radius of the big circle.

OO' + O'B = OB

OO' + O'B - O'B = OB - O'B

OO' + 0 = OB - O'B

OO' = OB - O'B

Notice that OB is equal to the radius of the big circle, so let that radius be R.

Notice also that O'B is equal to the radius of the small circle, so let that radius be r.

Therefore, OO' = OB - O'B = R - r

Using the two circles above that are tangent externally, draw the line between the centers of the circles and passing through the point of tangency Y.

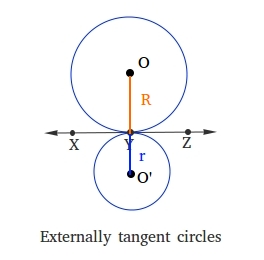
1. Line OO' is perpendicular to line XZ.

2. The distance between the centers of the two circles is equal to the distance (orange line) between the center of the big circle and the point of tangency plus the distance (blue line) between the center of the small circle and the point of tangency.

OO' = OY + YO'

Notice that OY is equal to the radius of the big circle, so let that radius be R.

Notice also that YO' is equal to the radius of the small circle, so let that radius be r.

Therefore, OO' = OY + YO' = R + r