Test for symmetry

This lesson will teach you how to test for symmetry. You can test the graph of a relation for symmetry with respect to the x-axis, y-axis, and the origin. In this lesson, we will confirm symmetry algebraically.

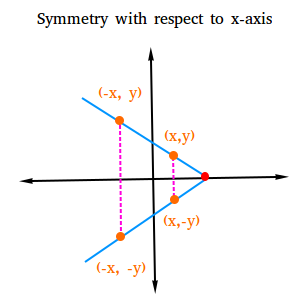
Test for symmetry with respect to the x-axis.

The graph of a relation is symmetric with respect to the x-axis if for every point (x,y) on the graph, the point (x, -y) is also on the graph. To check for symmetry with respect to the x-axis, just replace y with -y and see if you still get the same equation. If you do get the same equation, then the graph is symmetric with respect to the x-axis.

Example #1:

is x = 3y⁴ - 2 symmetric with respect to the x-axis?

Replace y with -y in the equation.

X = 3(-y)⁴ - 2

X = 3y⁴ - 2

Since replacing y with -y gives the same equation, the equation x = 3y⁴ - 2 is symmetric with respect to the x-axis.

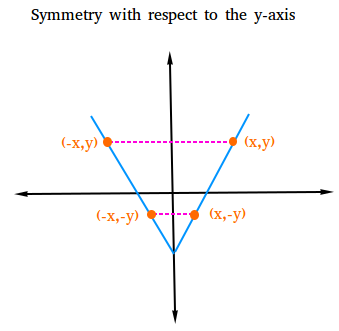
Test for symmetry with respect to the y-axis.

The graph of a relation is symmetric with respect to the y-axis if for every point (x,y) on the graph, the point (-x, y) is also on the graph.
To check for symmetry with respect to the y-axis, just replace x with -x and see if you still get the same equation. If you do get the same equation, then the graph is symmetric with respect to the y-axis.

Example #2:

is y = 5x² + 4 symmetric with respect to the x-axis?

Replace x with -x in the equation.

Y = 5(-x)² + 4

Y = 5x² + 4

Since replacing x with -x gives the same equation, the equation y = 5x² + 4 is symmetric with respect to the y-axis.

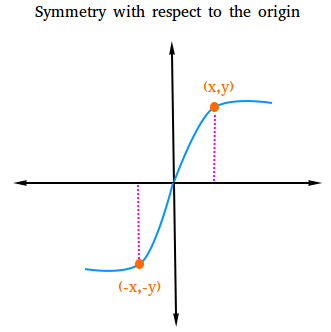
Test for symmetry with respect to the origin.

The graph of a relation is symmetric with respect to the origin if for every point (x,y) on the graph, the point (-x, -y) is also on the graph.
To check for symmetry with respect to the origin, just replace x with -x and y
with -y and see if you still get the same equation. If you do get the same equation, then the graph is symmetric with respect to the origin.

Example #3:

is 2xy = 12 symmetric with respect to the origin?

Replace x with -x  and y with -y in the equation.

2(-x × -y) = 12

2xy = 12

Since replacing x with -x and y with -y gives the same equation, the equation 
2xy = 12  is symmetric with respect to the origin.