Triangle midsegment theorem proof
The triangle midsegment theorem proof is easy to follow in this lesson. This lesson will give a coordinate proof of the triangle midsegment theorem. What is the triangle midsegment theorem?
If a segment joins the midpoints of the sides of a triangle, then the segment is parallel to the third side and the segment is half the length of the third side.
Here is the triangle midsegment theorem proof
Proof of the theorem.
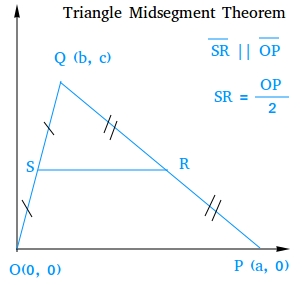
Consider the following triangle on the coordinate system.
|
Given: S is the midpoint of OQ R is the midpoint of PQ Prove: SR || OP
SR =
OP
2
|
 |
|
Given: S is the midpoint of OQ R is the midpoint of PQ Prove: SR || OP
SR =
OP
2
|
 |
To prove that SR || OP, we can just show that their slopes are equal.
|
S: (
b + 0
2
,
|
c + 0
2
)
|
= (
b
2
,
|
c
2
)
|
|
S: (
b + 0
2
,
|
c + 0
2
)
|
= (
b
2
,
|
c
2
)
|
|
R: (
a + b
2
,
|
c + 0
2
)
|
= (
a + b
2
,
|
c
2
)
|
|
R: (
a + b
2
,
|
c + 0
2
)
|
= (
a + b
2
,
|
c
2
)
|
Since the y-coordinate is the same for both points, the slope of SR is zero. The same is true for OP. Since the y-coordinate is the same, the slope is also zero. Since the slope is the same for SR and OP , SR || OP
To prove that SR is half OP, we can use the distance formula to find SR and OP.
| $$ OP = \ {\sqrt{(a - 0)^2 + (0 - 0)^2 } } $$ |
| $$ OP = \ {\sqrt{(a)^2 + (0)^2 } } $$ |
| $$ OP = \ {\sqrt{(a)^2 } } = a $$ |
| $$ SR = \ {\sqrt{(\frac{a+b} {2} - \frac{b} {2} )^2 + (\frac{c} {2} -\frac{c} {2} )^2 } } $$ |
| $$ SR = \ {\sqrt{(\frac{a} {2}+ \frac{b} {2} - \frac{b} {2} )^2 + (0)^2 } } $$ |
| $$ SR = \ {\sqrt{(\frac{a} {2} + 0)^2 + (0)^2 } } $$ |
| $$ SR = \ {\sqrt{(\frac{a} {2})^2 } = \frac{a} {2} } $$ |
Therefore, SR =
OP
2