What are Compatible Numbers? Definition and Examples
What are compatible numbers? Compatible numbers are numbers that look nice or friendly with each other when we do mental calculation to estimate a product, an addition, a subtraction, but especially a division. Take this quiz to see how much you know!
Compatible Numbers Quiz
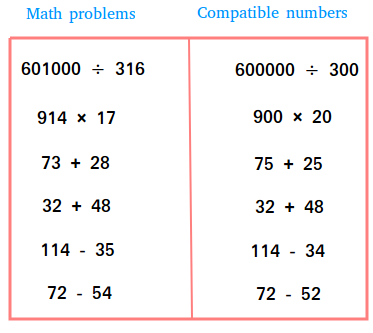
Using the figure above, we can make the following conclusions about compatible numbers:
Estimating Sums
- Fives are compatible: 75 + 25 = 100
- Any numbers that make tens are compatible. 32 + 48 = 80
Estimating Differences
- Numbers with the same final digit or digits are compatible: 72 - 52.
- Numbers that end with 1 or more zeros are compatible. For example, use 200 - 100 to estimate 198 - 99.
Estimating Products and Quotients.
- Numbers that end with 1 or more zeros are compatible.
- Numbers in the multiplication table assuming that we know the table by heart.
Some Examples of Compatible Numbers When Doing Division
- 400 and 10
- 36 and 6
- 2400 and 12
- 64 and 8
2400 and 12 are compatible because when doing this division (2400/12), we can quickly divide 24 by 12 to get 2 and put two zeros at the end to get 200.
Examples of Compatible Numbers When Doing Multiplication
- 200 and 40
- 1100 and 40
- 25 and 4
1100 and 40 are compatible because we can quickly do this multiplication by multiplying 11 and 4 to get 44 and add three zeros at the end to get 44000.
Examples of Compatible Numbers When Doing Addition
- 225 and 75
- 298 and 2
- 540 and 60
540 and 60 are compatible numbers because we can quickly add 40 and 60 to get 100. Then, you could just add 100 to 500 to 600.
Examples of Compatible Numbers When Doing Subtraction
- 435 and 25
- 800 and 600
- 5986 and 2986
5986 and 2986 are compatible numbers because it is quite easy to subtract 86 from 86 to get 00. Then, it is also easy to subtract 29 from 59 to get 30. The answer is 3000
When estimating, keep in mind that we are not claiming the answer will be exact. we are just looking for a reasonable estimate.
- When estimating with division, if you decrease the value of one number, you should also decrease the value of the other. If you increase the value of one number, you should increase the value of the other.
- When estimating with multiplication, if you decrease the value of one number, you would normally increase the value of the other. If you increase the value of one number, you should decrease the value of the other.
This helps to keep the estimate as close as possible to the exact answer.
Estimate Division using Compatible Numbers
1. 232 ÷ 11 2. 3421 ÷ 9 3. 25889 ÷ 52
1. 232 ÷ 11
- Compatible numbers for 232 and 11 are 240 and 12.
- 24 can be divided by 12 to get 2. Then, add a zero at the end to get 20
Notice that both numbers were increased!
2. 3421 ÷ 9
- Compatible numbers for 3421 and 9 are 3200 and 8.
- 32 can be divided by 8 to get 4. Then add one zero at the end to get 400
400 is a reasonable estimate since 3321 ÷ 9 = 369 and 369 can be rounded to the nearest hundred to 400.
3. 25889 ÷ 52
- Compatible numbers for 25889 and 52 are 25000 and 50
- When dividing 25000 by 50, the zero next to 50 cancels out with one zero of 25000, so the problem becomes 2500 ÷ 5
- 25 ÷ 5 = 5. Then, add two zeros at the end and the answer is 500
500 is a reasonable estimate because 25889 ÷ 52 = 497.86 and 497.86 is close to 500
Estimate Multiplication using Compatible Numbers
1. 72 × 78 2. 288 × 415
1. 72 × 78
- Compatible numbers for 72 and 78 are 70 and 80
- Multiply 7 by 8 and add two zeros at the end to get 5600
Note that one number was decreased while the other was increased!
2. 288 × 415
- Compatible numbers for 288 and 415 are 300 and 400
- Multiply 3 by 4 and add four zeros at the end to get 120000
Summary
Definition: Compatible numbers are "friendly" numbers that simplify mental calculations.
Applications: Useful for estimating sums, differences, products, and especially divisions.
Key Strategies:
- Use numbers that make tens for addition.
- Use numbers with the same final digit or ending with zeros for subtraction.
- Use numbers ending with zeros or from the multiplication table for multiplication and division.
- Ensure consistency when adjusting numbers for division estimates.
Now, if I ask the question again, what are compatible numbers, would you be able to answer with confidence? If not, just study again! So, what are compatible numbers? Just kidding!