Write the equation of a parabola
Learn how to write the equation of a parabola in vertex form using the graph of the parabola.
Example #1
Use the graph of the parabola below to write the equation of the parabola
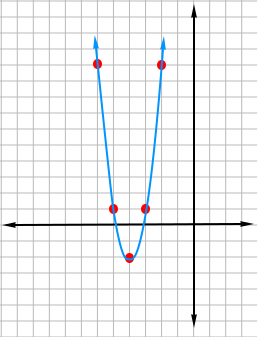
The vertex form of a parabola is y = a(x - h)2 + k, (h, k) is the vertex
Looking at the parabola above, the vertex is located at (h, k) = (-4, -2)
Substitute h = -4 and k = -2 into the vertex form.
y = a(x - h)2 + k
y = a(x - -4)2 + -2
y = a(x + 4)2 + - 2
Pick any point on the graph (except the vertex) and substitute the point into y = a(x + 4)2 + - 2 in order to find a.
Let us pick (-2, 10)
10 = a(-2 + 4)2 + - 2
10 = a(2)2 + - 2
10 = a(4) + - 2
Add 2 to each side of the equation
10 + 2 = a(4) + - 2 + 2
12 = 4a
Divide each side by 4
12/4 = 4a/4
a = 3
The equation of the parabola is y = 3(x + 4)2 + - 2
Notice that if you had picked (-3, 1) instead, you would have gotten the same answer.
1 = a(-3 + 4)2 + - 2
1 = a(1)2 + - 2
1 = a + - 2
a = 3
Example #2
Use the graph of the parabola below to write the equation of the parabola
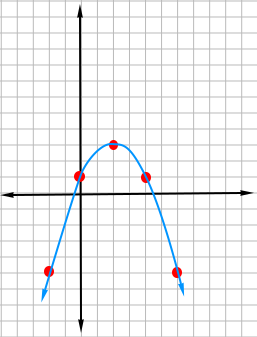
Looking at the parabola above, the vertex is located at (h, k) = (2, 3)
Substitute h = 2 and k = 3 into the vertex form.
y = a(x - h)2 + k
y = a(x - 2)2 + 3
Pick any point on the graph and substitute the point into y = a(x - 2)2 + 3 in order to find a.
Let us pick (-2, -5)
-5 = a(-2 - 2)2 + 3
-5 = a(-4)2 + 3
-5 = a(16) + 3
Subtract 3 from each side of the equation
-5 - 3 = a(16) + 3 - 3
-8 = a(16)
Divide each side by 16
-8/16 = a(16)/16
a = -1/2 = -0.5
The equation of the parabola is y = -0.5(x - 2)2 + 3