Absolute value function
An absolute value function is a function of the form f(x) = |mx + b| + c, where m ≠ 0
For example, f(x) = |2x - 3| + 1 is an absolute value function with m = 2, b = -3 and c = 1.
The graph of f(x) = |2x - 3| + 1 is shown below.
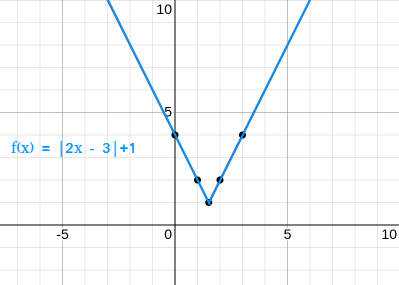
Just like the graph above, graphs of absolute value functions look like angles.
The vertex of a function is a point where the function reaches a minimum or a maximum.
The vertex of f(x) = |mx + b| + c is located at (-b / m, c).
For example, using the function f(x) = |2x - 3| + 1, the vertex is located at (--3 / 2, 1) or (3 / 2, 1).
(3 / 2, 1) is the same as (1.5, 1). Looking at the graph above, we can clearly see that the vertex is located at (1.5,1) and it is a minimum.
Other examples of absolute value functions
1. y = |x|
m = 1, b = 0, and c = 0
2. y = |x + 1|
m = 1, b = 1, and c = 0
3. y = |4x - 8| - 3
m = 4, b = -8, and c = -3
4. y = |-x|
m = -1, b = 0, and c = 0
5. y = |-x| - 8
m = -1, b = 0, and c = -8
6. y = |-3x + 5| - 4
m = -3, b = 5, and c = -4