Graph an absolute value function

You can quickly graph an absolute value function using the vertex and a table of values.

Note that the vertex is the sharp corner of the graph!

Example #1

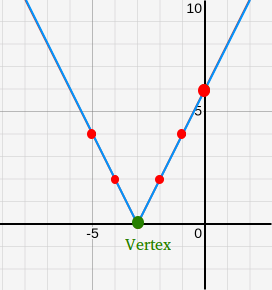
Graph f(x) = |2x + 6|

The general form of the function is f(x) = |mx + b| + c

Using f(x) = |2x + 6|, m = 2, b = 6, and c = 0

First, find the vertex.

As seen in the lesson about absolute value function, the vertex is located at (-b / m, c)

Therefore, the vertex is (-6 / 2, 0) or (-3, 0)

Now, evaluate the function for several selected values of x.

x	-5	-4	-2	-1	0
f(x)	4	2	2	4	6

The graph of the absolute value function is shown below

Example #2

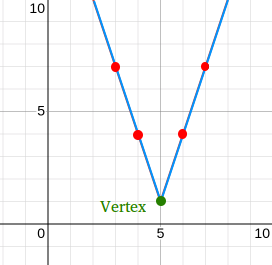
Graph f(x) = |-3x + 15| + 1

The general form of the function is f(x) = |mx + b| + c

Using f(x) = |-3x + 15| + 1, m = -3, b = 15, and c = 1

First, find the vertex.

The vertex is located at (-b / m, c) or (-15 / -3, 1) or (5, 1)

The vertex is (-6 / 2, 0) or (-3, 0)

Now, evaluate the function for several selected values of x.

x	3	4	6	7
f(x)	7	4	4	7

The graph of the absolute value function is shown below

Recent Articles