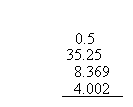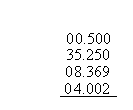Adding Decimals
Adding decimals is very similar to adding whole numbers. Let us start our lesson with something simple. Take a look at the following additions. You can clearly see that there isn't much difference between addition of decimals and addition of whole numbers. Nonetheless, there are some important rules to follow to make sure that you end up with the correct answer.
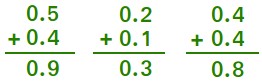
Rules to follow when adding decimals
Just follow the three rules below in the order they are listed here!
Rule #1
Make sure that the decimal numbers you are adding are like decimals. For example, 2.325 and 4.8 are not like decimals since they do not have the same number of decimal places or the same number of digits to right of the decimal point.
Just add zeros as placeholders until the decimals are like decimals. For example, just add two zeros as placeholders after 8 to get 4.800. Now, 2.325 and 4.800 have the same number of decimal places.
Rule #2
Once the decimals are in vertical format, the most important rule, in my opinion, is to align the decimal points and keep the digits with the same place value in the same column. This will ensure that you do not add tenths to hundredths or hundredths to thousandths and so forth...
Rule #3
If you have done rule #1 and rule #2, you are ready to add digits that have the same place value. Remember to carry numbers when necessary just like you do it when adding whole numbers.
Finally, do not forget to write the decimal point that is located between the digit in the ones place and the digit in the tenths place!
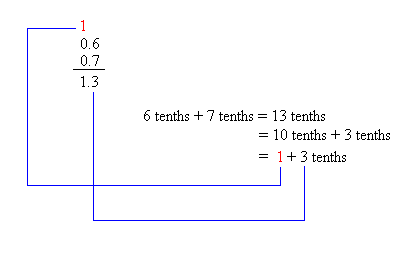
In the first addition problem, we are adding 0.5 to 0.4. Since rule #1 and rule #2 are already in place, just go straight to rule #3 by adding the digits.
- First, add the tenths (5 and 4) to get 9 tenths
- Then, add the ones (0 and 0) to get zero.
- Finally, write the decimal. It is placed immediately after the number in the ones place.
Now try to add the following decimals.

Notice that adding the tenths will give a number higher than 10 tenths or 1. Therefore, to add these decimals, we must carry over a 1 to the ones place. Recall also that 1 tenth = 0.1, so 10 tenths = 10 × 0.1 = 1
The following demonstrates how to add the first two problems:
To add 0.8 to 0.8, we do something similar

Try to do the last problem yourself and you will get 1.6 for an answer.
How to add decimals horizontally
You could have gotten the answers by adding horizontally.
0.6 + 0.7 = 0.6 + 0.4 + 0.3 = 1 + 0.3 = 1.3 (0.7 = 0.4 + 0.3)
0.8 + 0.8 = 0.8 + 0.2 + 0.6 = 1 + 0.6 = 1.6 (0.8 = 0.2 + 0.6)
0.9 + 0.7 = 0.9 + 0.1 + 0.6 = 1 + 0.6 = 1.6 (0.7 = 0.1 + 0.6)
In practice, when adding vertically, there is no need to write down all those tenths. You can pretend that the decimal point does not exist and try adding the decimals as if you were adding whole numbers.
Here is how if we are adding 0.6 to 0.7 and 0.8 to 0.8
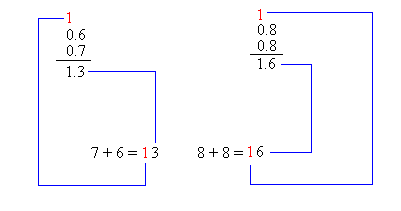
How to add decimals with whole numbers
You just need to follow rule #1 when you add decimals with whole numbers.
For example, add 42 and 3.0147 together.
42 = 42.0000 since we need to use four zeros as placeholders. Now 42.0000 and 3.0147 have the same number of digits after the decimal point.
42.0000
+ 3.0147
--------------------
45.0147
42 and 3.0147 = 45.0147
More examples showing how to add decimals
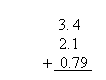
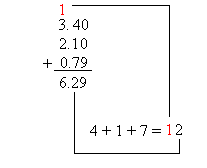
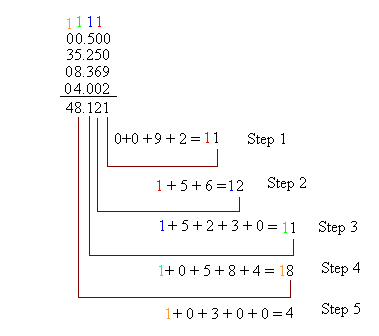
Now it is time to do a more challenging example. Add the following four decimal numbers: 0.5,35.25, 8.369, and 4.002