Adding Integers using an Interactive Number Line or the Rules for Addition of Integers
Interactive lesson for adding two integers on the number line
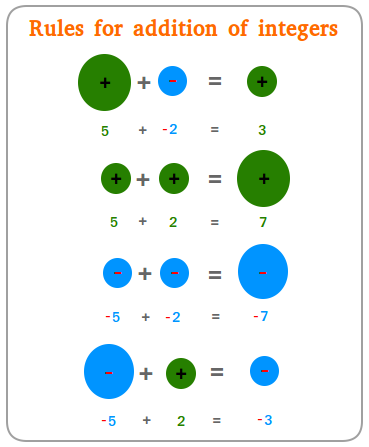
Rules for Adding Integers:
- Adding a positive number means moving right on the number line ⟶
- Adding a negative number means moving left on the number line ⟵
- Start at the first number, then move according to the second number
Adding integers is the process of getting the sum of two, three, or more integers. The sum of two or more integers could become smaller, bigger, or just equal to zero.
The addition of integers could be performed using any of the following methods:
- Using a number line
- Using the rules for adding integers shown in the figure below
- Using chips or counters to model the integers
The first two methods will be covered here in this lesson. See our related topics below if you want to learn how to add integers using chips or counters.
Adding integers using a number line
A number line is a good way to start when learning how to add integers. It will help you think through problems and approach them with intuition. As a result, the rules for addition of integers will make more sense and they will also be easier to remember.
Here are the two main things to remember when adding integers with a number line:
If you add a positive number, move in the positive direction (to the right).
If you add a negative number, move in the negative direction (to the left).
Example #1
Add: 2 + 6
Start at 2 and move 6 units to the right. Since you stopped at 8, the answer is 8.
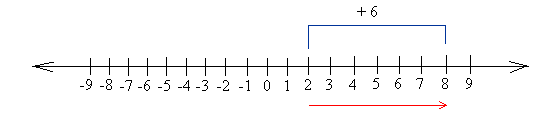
2 + 6 = 8
Notice that you will get the same answer if you start at 6 and move 2 units to the right.
Example #2
Add: -2 + 8:
Start at -2 and move 8 units to the right. Since you end up at 6, the answer is 6.
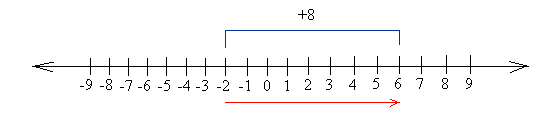
-2 + 8 = 6
Notice that you will get the same answer if you start at 8 and move 2 units to the left.
Example #3
Add: 4 + -7
Start at 4.
As already stated in example #2, the number you are adding to 4 is a negative number (-7 is negative), so you have to move 7 units to the left.
After you do that, you will end up at -3, so the answer is -3
4 + -7 = -3
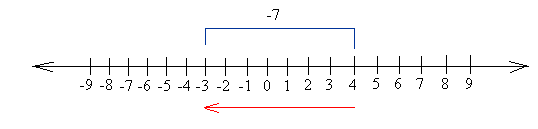
Notice that you will get the same answer if you start at -7 and move 4 units to the right.
Example #4
Add: -2 + -6
Start at -2
Once again, the number you are adding is a negative number (-6 is negative), so you will move 6 units to the left.
You will end up at -8, so the answer is -8.
-2 + -6 = -8
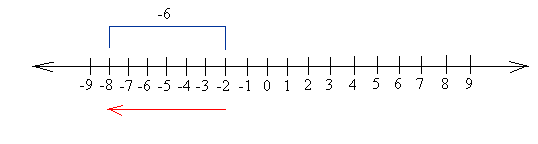
Notice that you will get the same answer if you start at -6 and move 2 units to the left.
Other examples showing how to add integers using a number line.
-1 + 8 = 7 ( Start at -1 and move 8 units to the right).
4 + -4 = 0 ( Start at 4 and move 4 units to the left).
7 + -9 = -2 ( Start at 7 and move 9 units to the left).
-5 + 3 = -2 ( Start at -5 and move 3 units to the right)
Problems than can arise when using a number line to add integers
What if you want to find the sum of the following integers?
-78 + 90
-520 + -144
-240 + 115
A couple of problems can come up
- First, your number line may not fit in your notebook
- Second, even if you could manage to fit the number line somewhere, since the numbers are so big, it will be very inconvenient or take a long time to count.
For example, starting from -78 and move 90 units to the right is very inconvenient. This is the reason that we need rules.
Rule for adding integers with the same sign
Rule #1
When adding integers with the same sign, add their absolute values. The sum has the same sign as the addends. For example, if you add two negative integers, the sign of the sum is still negative. Similarly, if you add two positive integers, the sign of the sum is still positive.
Example #4 revisited
Add: -2 + -6
Add the absolute value:
Absolute value of -2 = |-2| = 2
Absolute value of -6 = |-6| = 6
|-2| + |-6| = 2 + 6 = 8
The sum has the same sign as the addends.
Since the sign of the addends is negative (-), the sign of the sum is also negative (-)
-2 + -6 = -8
Rule for adding integers with different signs
Rule #2
When adding integers with different signs, find the difference of their absolute values. The sum has the same sign as the addend with the greater absolute value.
Example #3 revisited
Add: 4 + -7
Add the absolute value:
Absolute value of 4 = |4| = 4
Absolute value of -7 = |-7| = 7
|-7| - |4| = 7 - 4 = 3
The addend with the greater absolute value is -7 and -7 has a negative sign. Therefore, the sign of the sum is negative (-)
4 + -7 = -3
Adding integers using the rules for addition of integers
Earlier, we mentioned that it will be hard to do the following additions using a number line.
1) -78 + 90
2) -520 + -144
3) -240 + 115
Let us use the rules to do them now!
1) -78 + 90
|-78| = 78
|90| = 90
90 - 78 = 12
The addend with the greater absolute value is 90. Therefore, the sign of the sum is positive (+)
-78 + 90 = 12
2) -520 + -144
|-520| = 520
|-144| = 144
520 + 144 = 664
The sum has the same sign as the addends.
Since the sign of the addends is -, the sign of the sum is negative (-)
-520 + -144 = -664
3) -240 + 115
|-240| = 240
|115| = 115
240 - 115 = 125
The addend with the greater absolute value is -240. Therefore, the sign of the sum is negative (-)
-240 + 115 = -125
Other related topics related to integers are modeling integers with chips or counters, integers and inductive reasonings, and consecutive integers.