Addition rule for probability

Using the addition rule for probability, we will show you how to find the probability of the union of two events.

We will use the table below about students who are gifted and those who are not.

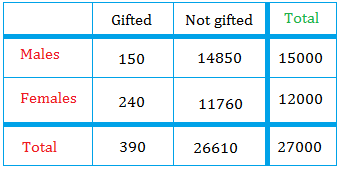
What is the probability that a randomly chosen student is gifted or male?

First, we need to know how many students are gifted or male. Let G = gifted and M = males

The number of students who are gifted or male is the union of G and M written as

G ∪ M

or

G or M

G ∪ M means either gifted, or male, or both.

To find  G ∪ M ,  we need to add the number of gifted students to the number of male students.

Gifted = 150 + 240

Males = 150 + 14850

Gifted + Males = 150 + 240 + 150 + 14850

However, notice that 150 is counted twice. So to avoid double counting, we need to subtract 150 from 150 + 240 + 150 + 14850

150 is the number of students who are gifted and male at the same or G ∩ M

If you don't subtract 150, you will end up counting G ∩ M  twice

The number students who are gifted or male is

G ∪ M = 150 + 240 + 150 + 14850 - 150 = 15240.

Let G ∪ M be the probability that a student is gifted or male.

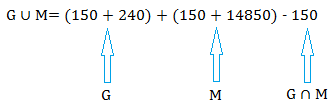
 G ∪ M   = G  + M -  G ∩ M

 Let us compute for the following  probability

 P(G ∪ M) = P(G)  + P(M) -  P(G ∩ M)

P(G ∪ M) = 0.014 + 0.555 - 0.005  = 0.569 - 0.005 = 0.564 

Addition rule for probability when the events are mutually exclusive

If A and B are mutually exclusive, it means that A ∩ B= { }

Thus, P(A and B) = 0

P(A or B) = P(A) + P(B)