Joint probability

The joint probability is the probability of the intersection of two events or the probability of two events happening together.

Let A and B be two events in a sample space.

The intersection of A and B is the collection of all outcomes that are common to both A and B.

We can denote the intersection of A and B as  A ∩ B or  AB.

The probability of A and B happening together is P(A ∩ B)

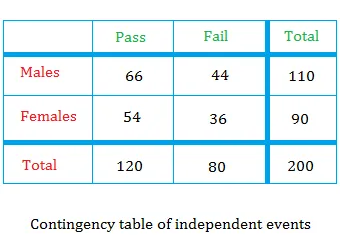
Take a look at the contingency table of independent events.

Pass = {66, 54}  and Males = {66, 44}

Pass ∩ Males = {66}

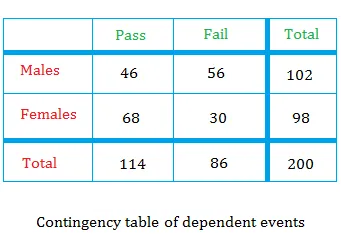
Now how do we compute the joint probability? Using the two tables below, we will compute P(pass / male)

Contingency table of independent events
Contingency table of dependent events

Here is what we found In the lesson about probability of independent events.

Using the contingency table of independent events

P(pass / male) =
66 / 110

Using the contingency table of dependent events

P(pass / male) =
46 / 102

There is another way to find these answers.

Did you notice this using the table of independent events?

$$ \frac{\frac{66} {200}} {\frac{110} {200}} = \frac{66} {200} × \frac{200} {110} = \frac{66} {110} $$

Did you notice this using the table of dependent events?

$$ \frac{\frac{46} {200}} {\frac{102} {200}} = \frac{46} {200} × \frac{200} {102} = \frac{46} {102} $$

In conclusion, 

$$ P(pass / male) = \frac{\frac{66} {200}} {\frac{110} {200}} $$

In conclusion, 

$$ P(pass / male) = \frac{\frac{46} {200}} {\frac{102} {200}} $$
Joint probability
P(pass and male) =
66 / 200
P(pass and male) =
46 / 200


P(male) =
110 / 200
P(male) =
102 / 200

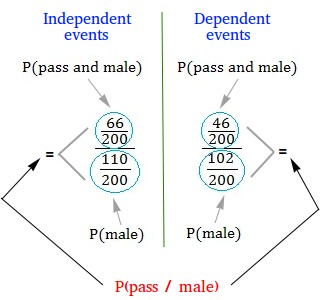
As you can see, it does not matter if the events are independent or not, the formula is

P(pass / male) =
P(pass and male) / P(male)

Multiplication rule of joint events


Multiply both sides of the equation immediately above by P(male)

P(male) × P(pass / male) =
P(pass and male) / P(male)
× P(male)

P(male) × P(pass / male) = P(pass and male)

P(pass and male )  = P(male) × P(pass / male)

In general, if A and B is the intersection of two events.

P(A and B) = P(A) × P(B / A)  or P(A and B) = P(B) × P(A / B)

Joint probability of independent events


If A and B are independent events, we know that P(A) = P(A / B)  or  P(B) = P(B / A)

P(A and B) = P(A) × P(B / A).

Since  P(B / A) = P(B), P(A and B) = P(A) × P(B)

Joint probability of mutually exclusive events


The joint probability of two mutually exclusive events is always zero.

When two events A and B are mutually exclusive, A ∩ B = { }

In other words, the intersection is empty. Since the intersection is empty, the probability zero.

Probability of complementary events