Area between four touching circles

This lesson will help you understand clearly how to find the area between four touching circles. First, we need to show you what the area between four touching circles looks like.

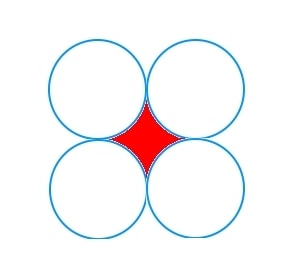
The area in red above is the area between the four touching circles. To find it, label the figure as shown below. Notice that all the circles have the same radius that is x. Therefore, we are assuming here that the circles are congruent or equal.

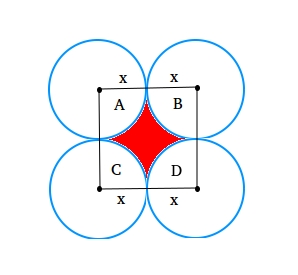
Let x be the radius of each circle.

Let A be a sector or that part of a circle bounded by two radii and their intercepted arc. Therefore, B, C, and D are also sectors.

Here is the important or crucial observation you need to make to solve this problem.

area of sector A + area of sector B + area of sector C + area of sector D + area of red piece = area of the square

Since area of sector A = area of sector B = area of sector C = area of sector D

area of sector A + area of sector B + area of sector C + area of sector D =  area sector A + area of sector A + area of sector A + area of sector A = 4 times area of sector A.

We can rewrite the part in blue and red as

4 times area of sector A + area of red piece  =  area of square

Area of red piece = area of square  - 4 times area of sector A

Area of square = side times side = (x + x) times ( x + x) = 2x times 2x = 4x²

4 times area of sector A = 4 times [ ( 3.14 times x² ) / 4 ] = 3.14 times x²

Therefore, area of red piece  =   4x²  - 3.14x²

                                                 = ( 4 - 3.14) x²           

                                                 = 0.86 x²

Area between four touching circles examples

Example #1

Suppose the radius is equal to 5 cm, what is the area between the four touching circles?

Area  = 0.86x²

Area = 0.86 times 5 cm times 5 cm

Area = 0.86 times 25 = 21.5 cm²

Example #2

Suppose the radius is equal to 8 feet, what is the area between the four touching circles?

Area  = 0.86x²

Area = 0.86 times 8 feet times 8 feet

Area = 0.86 times 64 = 55.04 ft²