Area of a Circle
The area of a circle is the space taken by the circle in a two-dimensional plane. In the figure below, notice that the space occupied or taken by the circle on the left is less. Therefore, the area of the smaller circle on the left is less.
Area of circle formula
The most common way to find the area of a circle is to use the formula shown below in blue.
A = pi × r2 = π × r2
A = area
pi or π is a special mathematical constant, and it is approximately equal to 22/7 or 3.14.
Pi is also the ratio of a circle's circumference to its diameter. If you want to know why pi is used in the formula to find area of a circle, check this lesson about the number pi to get the full answer.
If r or the radius of a circle is known, you simply need to multiply 3.14 by the square of the radius.
The area is expressed in square units.
- If r is measured in meters, then the area is measured in square meters or m2.
- If r is measured in centimeters, then the area is measured in square centimeters or cm2.
- If r is measured in inches, then the area is measured in square inches or in.2
What is the surface area of a circle?
Here is something important to keep in mind!
The surface area of a circle is absolutely the same as the area of the circle. Surface area is an expression that is usually associated with 3-D figures such as a sphere. Since a circle is not a 3-D figure, "area" and "surface area" refer to the same thing.
To find the surface area, just use any of the formulas discussed in this lesson.
There are three ways to find the area of a circle
- You can use the radius of a circle
- You can use the diameter of a circle
- You can use the circumference of a circle
How to find the area of a circle using the radius
The radius of a circle is the distance from the center of the circle to a point on the circle. Once you know this distance, you simply need to substitute the known value for r in the formula.
Area = π × r2
Example #1
Using the area of a circle formula, calculate the area if the radius is 4 inches.
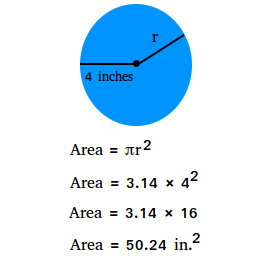
Notice that the unit (inches) is squared to show that it was multiplied by itself twice.
Example #2
Calculate the area if the radius is 6 inches.
Area = pi × r2 = 3.14 × 62 = 3.14 × 36 = 113.04 in.2
How to find the area of a circle using the diameter
The formula to use if you know the diameter of the circle is area = (πd2) / 4, d is the diameter. The diameter of a circle is the distance from one point on the circle to another point on the circle and passing through the center of the circle. The diameter is twice as big as the radius. Once you know this distance, you simply need to substitute the known value for d in the formula.
Example #3
Calculate the area of the circle if the diameter is 20 cm.

Next, we show you how to express the formula in terms of diameter.
|
r × r =
d
2
|
×
d
2
|
|
r × r =
d
2
|
×
d
2
|
Let's us use the formula right above to find the area.
A = 3.14 × 100
A = 314 cm2
The other way to solve example #3 is to get r and then replace its value.
Since r is half the diameter, r = 20 divided by 2.
r = 10 cm
A = pi × r2 = 3.14 × 102 = 3.14 × 100 = 314 cm2
How to find the area of a circle in terms of circumference
The formula to use if you know the circumference of the circle is area = (circumference)2 / 4π.
First, let us quickly derive the formula that is (circumference)2 / 4π.
Let C be the circumference. The formula to use to find the circumference of a circle, also called length of its boundary is C = 2πr then r = C / 2π.
Substitute C / 2π for r in the area formula
Area = π × r2 = π × r × r
Area = π × C / 2π × C / 2π
Area = π / 1 × C / 2π × C / 2π
Area = (π × C × C) / 1 × 2π × 2π
Area = (π × C2) / (4π × π)
Cancel π
Area = C2 / 4π
Example #4
Calculate the area of the circle if the circumference is 157.079 meters
Area = 157.0792 / 4(3.14)
Area = 24673.812 / 12.56
Area is approx. 1964 m2
Examples #5
If A = 78.5 in.2, find r or the radius of the circle
Review solving multiplication equations before looking at the solution below.
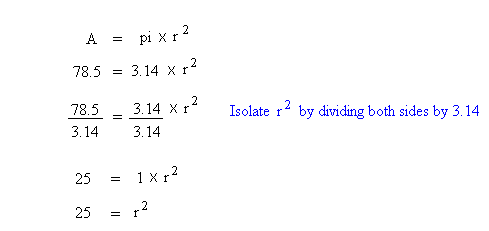
How to derive the area of a circle
Draw a large circle using a compass. Draw two diameters, one that is horizontal and the other vertical. Fold the circle vertically and horizontally. Then, cut or slice the circle into four wedges on the fold lines.
Cut each wedge into 4 equal sections. The total number of sections is 16. Use the 16 wedges or sections to make the figure below looking "somewhat" like parallelogram.
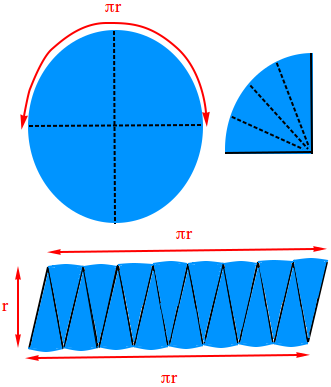
The base of the figure is formed by arcs of the circle. You need 8 arcs (8 sections) to form the base.
Notice that 8 arcs is equivalent to half the circumference of the circle. The more you increase the number of wedges, the more the figures you create will look like rectangles with base π × r and height r.
The area of these rectangles is base × height = π × r × r = π × r2
Circle calculator
Learn how to approximate the area of a circle
Learn how to compute the area of a sector using the central angle