Area of a sector

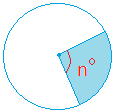
A sector is part of a circle bounded by two radii and their intercepted arc. Examples of sectors are illustrated below. The portion of the circle shaded in blue is the sector.

The best real life example of a sector I can think of is a slice of pizza.

In the example above, one-fourth of the pizza is removed and we can call it a sector. Next time you talk to a friend, you can tell them that you ate a sector of a pizza. Just kidding!

Therefore, to get the area of this slice of pizza, you will need to find the area of the circle and then divide the result by 4.

Visualizing things this way may make it a little easier to see how they arrived to the formula.

What does the formula look like when n is equal to 360 degrees?

Notice that 360° / 360° = 1 and 1 × π × r² = π × r².

What does the formula look like when n is equal to 180 degrees?

What does the formula look like when n is equal to 90 degrees?

Therefore, in general, you can conclude that the formula to find the area of a sector is: 

A = n° 360° × π × r2

Caution when calculating the area of a sector: n must be positive and n must be less than 360 degrees

Example #1:

A circle has a radius of 5 cm. Calculate the area of a sector when the angle made by the radii is 60°







A = 0.166 × 78.5 = 13.06 cm²


Example #2:

A pizza has a diameter of 14 inches.

a. Calculate the area of a slice of pizza when the chef made all the slices with an angle of 45°

b. How many slices you think this pizza has?

c. Without using the formula of the area of a circle, what is the area of the whole pizza?







A = 0.125 × 615.44 = 76.93 inches²

b. If all slices were cut with the same angle, then all slices must have the same size.

Just ask yourself "How many 45° will give 360°?"

45° + 45° + 45° + 45° + 45° + 45° + 45° + 45° = 360°

Or 8 × 45° = 360°

The pizza has 8 slices

c. Since the pizza has 8 slices, the area of the whole pizza is 8 × 76.93 inches² = 615.44