Area of a Triangle Given SAS
This lesson will show you how to find the area of a triangle given sas. Suppose you are trying to find the area of the triangle below.
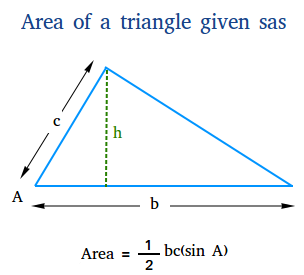
In order to use the formula above, we need to know what the height is. Thus, let us write an expression that will have the height in it. The sine ratio will help you achieve this.
Solve for h by multiplying both sides by c.
h = c(sin A)
Substitute c(sin A) for h in the formula for the area shown above.
The formula above shows that when you know the values of two sides and the value of the angle between these two sides, you have enough information to find the area of the triangle.
An example showing how to find the area of a triangle given sas
Example #1
A backyard is shaped like a triangle. The lengths of two adjacent sides of the triangular backyard are 50 feet and 65 feet. The angle between the sides is 30 degrees. Find the area of the backyard.
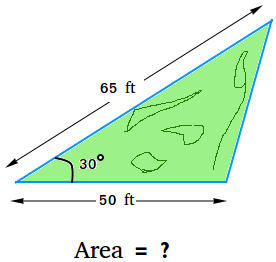
Let b = 50 feet, c = 65 feet, A = 30 degrees, and sin (30 degrees) = 0.5
Area = 25 × 65 × 0.5
Area = 25 × 32.5
Area = 812.5 ft2
Notice that sin(90 degrees) = 1 if the measure of the angle between the two sides is equal 90 degrees.
h = c(sin A)
h = c(sin 90 degrees)
h = c(1)
h = c
This result makes sense since you are dealing with a right triangle. In a right triangle c and the height are the same.