Base five numeration system

The main difference between base five numeration system and our familiar base 10 numeration system is that grouping is done in groups of 5 instead of 10. For instance, to represent 24 in base 10 using sticks, you could use two groups of ten and 4 as shown below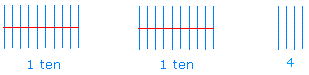
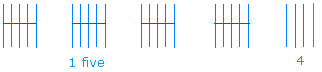
However, to represent the same number in base 5, you make groups of 5.

Notice that you have 4 groups of five and 4. You write 44_five or 44₅

Thus, 24₁₀ = 44₅

Be very careful when you read 44_five! You don't read it as forty four because this is how you read four tens and four in base 10. We are not in base 10 anymore.

44₅ is read four four base 5

In like manner, if you group 17 in groups of five, you can get three groups of 5 and 2

You write 17₁₀ = 32₅ and 32₅ is read three two base 5

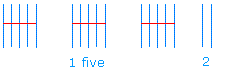
Look at the following pattern:

19₁₀ = 34₅

18₁₀ = 33₅

17₁₀ = 32₅

16₁₀ = 31₅

15₁₀ = ?

What do you think 15 is in base 5?

Yes, 15₁₀ = 30₅ = ?

This is important. It is not 3 just because we have three fives in 15

In fact, what it means is three fives in the second place value and zero number in the first place value

The first ten base 5 numerals are shown below:

1₅         2₅

3₅         4₅

10₅       11₅

12₅       13₅

14₅       20₅

Notice that the first four numbers have the same representation in base 10 and in base 5

The second difference between base five and base ten is that in base ten, we use the 10 digits 0, 1, 2, 3 , 4 , 5, 6, 7, 8, and 9

In base 10, when you have 10 tens, you replace it by one hundred and starting from the right one hundred is in the third position

In general, place values are power of 10: 10⁰ = 1, 10¹ = 10, 10² = 100, 10³ = 1000, etc. representing first, second, third place etc respectively.

On the other hand,

In base 5, we use only 5 digits 0, 1, 2, 3 , and 4

In base five, when you have 5 fives, you replace it by one twenty five and starting from the right twenty five is in the third position

In this case, place values are power of 5: 5⁰ = 1, 5¹ = 5, 5² = 25, 5³ = 125, etc representing first, second, third place etc.respectively..

Having said that, what is 57 in base 5

Group 57 in groups of 25 and 5

57 has 2 groups of 25, 1 group of 5 and 2, so 57₁₀ = 212₅