Binary number system

A binary number system is a base-2 positional numbering system that was invented by Gottfried Wilhelm Leibniz in the 17th century. In the base-2 numeral system, the radix is 2 since only two digits, 0 and 1 are used to represent all possible numbers.

The two digits 0 and 1 are frequently called bits, a contraction of the words binary digits.

For example, 11001₂ is a binary number.

The number of bits is 5 since 11001₂ has 5 digits.
Every digit in a binary number is therefore a bit. For example, the 1 on the left is a bit in the number 11001₂.
The 1 on the right is called the Least Significant Bit (LSB)
The 1 on the left is called the Most Significant Bit (MSB)

How to convert from decimal to binary

Method #1:

11001₂ is 25 as a decimal number. To convert 25 to the binary number system, we need to write 25 in expanded form while making sure that each addend can be written as a power of two.

25 = 16 + 8 + 1 = 2⁴ + 2³ + 2⁰

To make 25, we need 1 group of 16, 1 group of 8, 0 group of 4, 0 group of 2, and 1.

Starting from right to left, 1 goes in the first place(2⁰), 0, goes in the second place(2¹), 0 goes in the third place(2²), 1 goes in the fourth place(2³), and 1 goes in the fifth place(2⁴) as shown in the figure below.

25 in binary is 11001₂

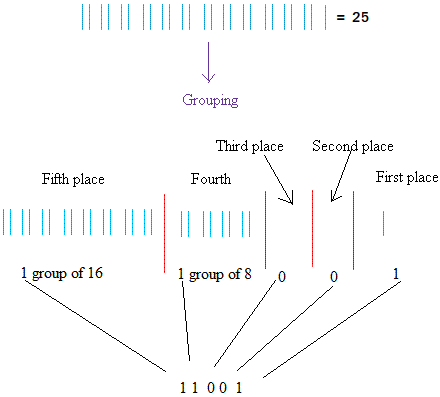
Notice that there are no groupings of two and four. As a result, put zeros in the second place and the third place.

How grouping is done in the binary number system. General guidelines to follow when converting from base 10 to base 2

Group from the nth place to the first place. This means that you have to create first a group with the highest possible power of 2.

For instance, I am trying to convert 45 to a binary number system. Ask yourself, "What is the highest power of 2 less than 45?"

2⁶ = 64. 2⁵ = 32. So, the highest power of 2 less than 45 is 2⁵ = 32

Since 32 goes in the sixth place, put 1 in the sixth place. Then try to find out what goes into the place value before.

45 - 32 = 13

Ask yourself, "What is the highest power of 2 less than 13?"

2⁴ = 16. 2³ = 8. So, the highest power of 2 less than 13 is 2³ = 8

Since 8 goes in the fourth place, put 1 in the fourth place. Then try to find out what goes into the place value before.

13 - 8 = 5

Ask yourself, "What is the highest power of 2 less than 5?"

2³ = 8. 2² = 4. So, the highest power of 2 less than 5 is 2² = 4

Since 4 goes in the third place, put 1 in the third place. Then try to find out what goes into the place value before.

5 - 4 = 1 and 1 goes into the first place.

Notice that you put nothing into the fifth place and the second place, so zeros go in those places.

Therefore, 45 converted to the binary number system is 101101.

You can also write 45_ten or 101101_two

Be very careful when you read 101101_two!

101101₂ is read one zero one one zero one base 2.

Method #2:

Step 1

Divide the dividend 25 by 2 and write the division algorithm.

Step 2

Use the quotient obtained in step 1 as the new dividend. Divide the new dividend by 2 and write the division algorithm again. Keep doing this until the quotient is 0.

Using method #2, here is how to convert the decimal number 25 into a binary number.

25 = 2 x 12 + 1

12 = 2 x 6 + 0

6 = 2 x 3 + 0

3 = 2 x 1 + 1

1 = 2 x 0 + 1

Write all the remainders obtained from bottom to top as 110001₂

Binary to Decimal conversion table
Binary	Decimal	Binary	Decimal
0	0	10000	16
1	1	10001	17
10	2	10010	18
11	3	10011	19
100	4	10100	20
101	5	10101	21
110	6	10110	22
111	7	10111	23
1000	8	11000	24
1001	9	11001	25
1010	10	11010	26
1011	11	11011	27
1100	12	11100	28
1101	13	11101	29
1110	14	11110	30
1111	15	11111	31

Similarity and difference between the decimal number system and the binary number system

The main difference between the binary number system and our familiar base 10 numeration system is that grouping is done in groups of 2 instead of 10.

For instance, to represent 24 in base 10 using sticks, you could use two groups of ten and 4 as shown below.

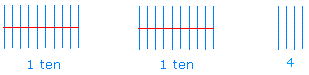
There is something important though to keep in mind and this is the key to fully understand this lesson!

The digits 0,1,2,3,4,5,6,7,8,9 are used to represent all possible numbers. Notice that base 10 has 10 digits, so the radix is 10.

Depend on how big the number is, we make groups of ten, hundred, thousand, ten-thousand, etc... (These are power of 10: 10¹ = 10, 10² = 100, 10³ = 1000)

If a number is less than 10 for example 8 and 9, the number will occupy the ones place value.

If a number is bigger than 9 and less than 100 for example 10, 55 and 98, group(s) of ten will occupy the tens place value.

If a number is bigger than 99 and less than 1000 for example 100, 255 and 999, group(s) of hundred will occupy the hundreds place value.

And so forth...

For example, carefully study the following number to see how it was organized.

Since the number is bigger than 99, we had to make groups of hundred and ten. Notice also how groups of hundred are put in the hundreds place value and groups of ten are put in the tens place value.

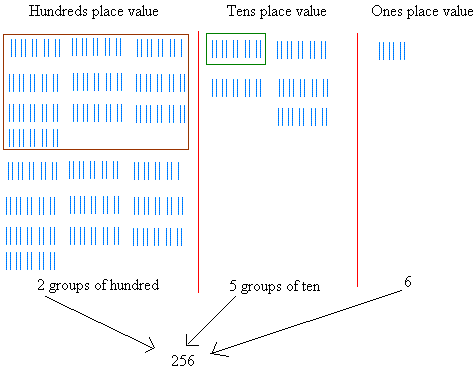
In a similar way, the binary number system has its own place value.

The digits 0,1 are used to represent all possible numbers in the binary number system. Notice that base 2 has 2 digits to represent all possible numbers.

Depend on how big the number is, we make groups of 2, 4, 8, 16, 32 etc...(These are power of 2: 2¹ = 2, 2² = 4, 2³ = 8)

If a number is less than 2 for example 1 there is no need to create groups. And this number will occupy the first place value. This place value correspond to the ones place in base 10. In fact this 1 is the same in the binary system and the base 10 system.

If a number is bigger than 1 and less than 4 for example 2 and 3, one group of two will occupy the second place value. You could also call it "two" place value.

If a number is bigger than 3 and less than 8 for example 4 and 7, one group of four will occupy the third place value. You could also call it "four" place value

If a number is bigger than 7 and less than 16 for example 8, 11, and 14, one group of eight will occupy the fourth place value. You could also call it "eight" place value.

If a number is bigger than 15 and less than 32 for example 16, 21, and 30, one group of sixteen will occupy the fifth place value. You could also call it "sixteen" place value.

If a number is bigger than 31 and less than 64 for example 32, 45, and 63, one group of thirty-two will occupy the sixth place value. You could also call it "thirty-two" place value.

And so forth...

Since we are only using 0 and 1 to represent numbers, it will not be possible to write binary numbers using the number 2 or any number higher than 2.

Applications of the binary number system

The base-2 numeral system has many applications in computer technology. For example, every computer ever built stores data such as numbers, graphics, and letters internally using the binary numbering system.

In every computer, there is usually a maximum number of bits that are used to store integers. Nowadays, the value is usually 16, 24, or 32 bits. However, many of the computers made in the 1970s used only 8 bits to store data.

8 bits has eight 1's and it is the binary number 11111111₂

11111111₂ = 2⁷ + 2⁶ + 2⁵ + 2⁴ + 2³ + 2² + 2¹ + 2⁰ = 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255.

With an 8-bit computer, any operation on the computer that produces an integer value greater than 255 will create an error since all of the memory locations are used up. A 16-bit computer though can produce an integer with a maximum value of 65535. You can see why there was a need to create computers that can store more data.