Calculating percent error
When calculating percent error, just take the ratio of the amount of error to the accepted value or true value, or real value. Then, convert the ratio to a percent. We can express the percent error with the following formula shown below: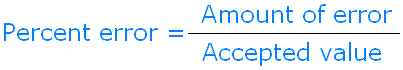
Keep in mind that when computing the amount of error, you are always looking for a positive value.
Therefore, always subtract the smaller value from the bigger. In other words, amount of error = bigger − smaller
Percent error word problem #1
A student made a mistake when measuring the volume of a big container. He found the volume to be 65 liters.
However, the real value for the volume is 50 liters. What is the percent error?
Percent error = (amount of error)/accepted value
amount of error = 65 - 50 = 15
The accepted value is obviously the real value for the volume, which 50
So, percent error = 15/50
Just convert 15/50 to a percent. We can do this multiplying both the numerator and the denominator by 2
We get (15 × 2)/(50 × 2) = 30/100 = 30%
Notice that in the problem above, if the true value was 65 and the measured value was 50, you will still do 65 − 50 to get the amount of error, so your answer is still positive as already stated.
Percent error word problem #2
A man measured his height and found 6 feet. However, after he carefully measured his height a second time, he found his real height to be 5 feet.
What is the percent error the man made the first time he measured his height?
Percent error = (amount of error)/accepted value
amount of error = 6 - 5 = 1
The accepted value is the man's real height or the value he found after he carefully measured his height, or 5
So, percent error = 1/5
Just convert 1/5 to a percent. We can do this multiplying both the numerator and the denominator by 20
We get (1 × 20)/(5 × 20) = 20/100 = 20%
I hope what I explained above was enough to help you understand what to do when calculating percent error
Any questions? Contact me.