Centroid of a triangle

The centroid of a triangle is the point where the three medians of a triangle meet or intersect. An illustration of the centroid is shown below.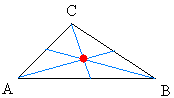

In the above graph, we call each line (in blue) a median of the triangle.

The median is the line that starts from a vertex and goes to the midpoint of the opposite side

After you construct all three medians, the point where they intersect ( shown in red ) is the centroid

Now, If you put a triangle on the coordinate system, you can easily get the centroid by doing some simple calculation




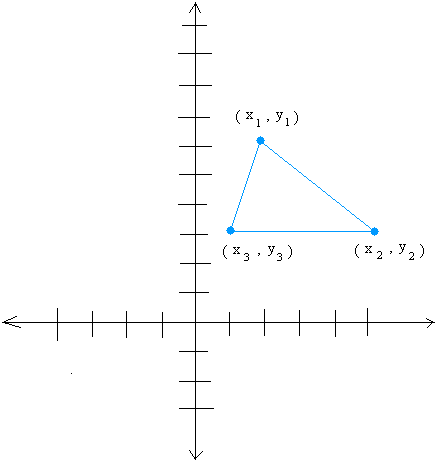
Call the centroid C, the formula to get the centroid is:

[( x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3]

Example:

Find the centroid of the following triangle with vertices (1,2), (3,4), and (5,0)




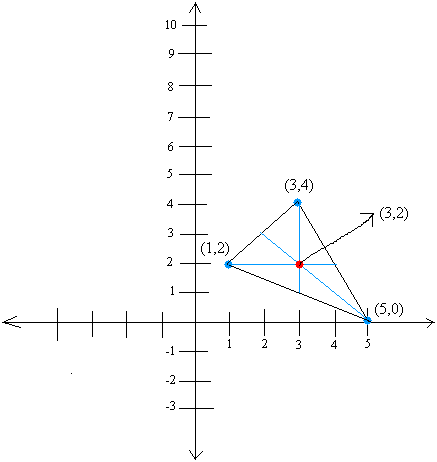
C = [ (1 + 3 + 5) / 3 , (2 + 4 + 0) / 3 ] = (9/3 , 6/3) = (3,2)