Midpoint of a line segment

To find the midpoint of a line segment on the coordinate system, simply take the average of the x-coordinates and the average of the y-coordinates.

Let (x₁ , y₁) and (x₂ , y₂) represent the endpoints of a line segment.

Therefore, the formula to get the midpoint is: [(x₁ + x₂) ÷ 2 , (y₁ + y₂) ÷ 2]

A couple of examples showing how to find the midpoint of a line segment

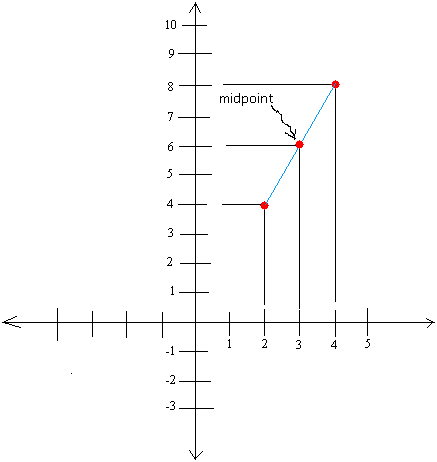
Example #1:

Graph (2, 4) and (4, 8) and find the midpoint

[(x₁ + x₂) ÷ 2 , (y₁ + y₂) ÷ 2] = [(2 + 4) ÷ 2, (4 + 8)÷ 2]

[(x₁ + x₂) ÷ 2 , (y₁ + y₂) ÷ 2] = (6 ÷ 2, 12 ÷ 2)

[(x₁ + x₂) ÷ 2 , (y₁ + y₂) ÷ 2] = (3, 6)

The graph is shown below.



Example #2:

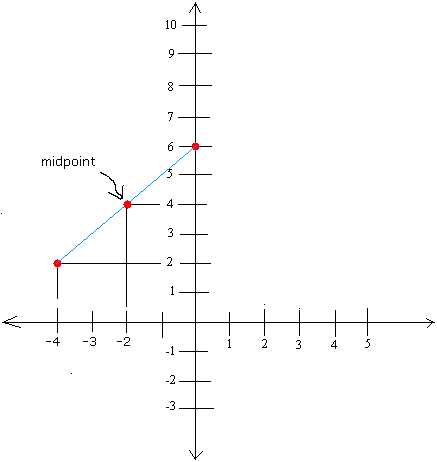
Graph (-4, 2) and (0, 6) and find the midpoint.

[(x₁ + x₂) ÷ 2 , (y₁ + y₂) ÷ 2] = [(-4 + 0) ÷ 2, (2 + 6)÷ 2]

[(x₁ + x₂) ÷ 2 , (y₁ + y₂) ÷ 2] = (-4 ÷ 2, 8 ÷ 2)

[(x₁ + x₂) ÷ 2 , (y₁ + y₂) ÷ 2] = (-2, 4)

The graph is shown below:



Example #3:

Using (5, -5) and (-1, 1), find the midpoint.

[(x₁ + x₂) ÷ 2 , (y₁ + y₂) ÷ 2] = [(5 + -1) ÷ 2, (-5 + 1)÷ 2]

[(x₁ + x₂) ÷ 2 , (y₁ + y₂) ÷ 2] = (4 ÷ 2, -4 ÷ 2)

[(x₁ + x₂) ÷ 2 , (y₁ + y₂) ÷ 2] = (2, -2)

Example #4:

Using (12, 0) and (-12, 2), find the midpoint.

[(x₁ + x₂) ÷ 2 , (y₁ + y₂) ÷ 2] = [(12 + -12) ÷ 2, (0 + 2)÷ 2]

[(x₁ + x₂) ÷ 2 , (y₁ + y₂) ÷ 2] = (0 ÷ 2, 2 ÷ 2)

[(x₁ + x₂) ÷ 2 , (y₁ + y₂) ÷ 2] = (0, 1)