Chebyshev's Theorem
Chebyshev's theorem will show you how to use the mean and the standard deviation to find the percentage of the total observations that fall within a given interval about the mean.
Important stuff to keep in mind about the Chebyshev's theorem
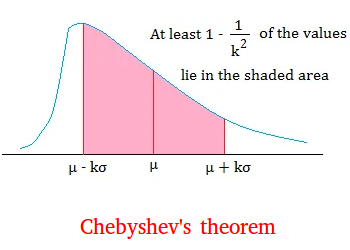
Take a look at the figure below and make the following observations:
The distance between µ and µ + kσ is kσ since µ + kσ - µ = kσ
The distance between µ and µ - kσ is kσ since µ - (µ - kσ ) = µ - µ - - kσ = 0 - - kσ = kσ
Notice that we say that k is greater than 1 or at least 2. k must be 2 because we get 0 when k = 1.
(1 −
1
k2
)
|
= (1 −
1
12
)
|
= (1 −
1
1
)
|
How to find standard deviation using Chebyshev's theorem
Let us now see how we can use Chebyshev's theorem.
Suppose you want to find the percent of values of a data set that lie within 2 standard deviations of the mean.
Just replace k = 2 into the formula.
(1 −
1
k2
)
|
= (1 −
1
22
)
|
= (1 −
1
4
)
|
0.75 as a percent is 75%
Therefore 75% of the values of a data set lie within 2 standard deviations of the mean.
How do we use the mean and the standard deviation to find the percentage of the total observations that fall within a given interval about the mean?
Suppose µ = 39 and σ = 5, find the percentage of values that lie within 29 and 49 of the mean.
29 -------------------- 39 -------------------- 49
We just need to find k and there are 2 ways to do so.
First, as we said earlier, notice that the distance between 39 and 49 is equal to kσ
Since the distance between 39 and 49 is 10, kσ = 10
kσ = 10
σ = 5, so 5k = 10
Since 5 times 2 = 10, k = 2.
We have already computed the percentage earlier when k = 2. We found that it was 75%.
Therefore, 75% of the values lie within 29 and 49 of the mean.
The second way to find the answer is to notice that µ + kσ = 49
29 ----------------- 39 ----------------- 49
µ - kσ µ µ + kσ
µ + kσ = 49
39 + kσ = 49
39 - 39 + kσ = 49 - 39
0 + kσ = 10
kσ = 10
5k = 10 and k = 2