Empirical rule

Just like the Chebyshev's theorem, the empirical rule can also be used to find the percentage of the total observations that fall within a given interval about the mean.

Here is the empirical rule:

About 68% of all the values lie within 1 standard deviation of the mean.

About 95% of all the values lie within 2 standard deviations of the mean.

About 99.7% of all the values lie within 3 standard deviations of the mean.

An illustration is shown below:

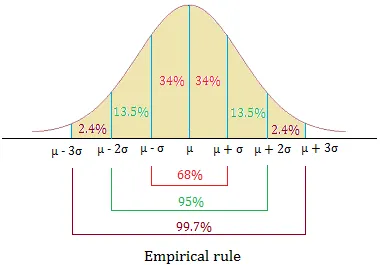
Notice that 34% + 34% = 68% and 34% + 34% + 13.5% + 13.5% = 95%

However, the empirical rule has its limitations just like Chebyshev's theorem. What is the difference between Chebyshev's theorem and the empirical rule?

With Chebyshev's theorem, you cannot find the percentage of the values of a data set that lie within one standard deviation the mean.

However, you can apply the theorem to any kind of distribution.

You can only use the empirical rule to a specific type of distribution called bell-shaped distribution or normal curve.

You can also use the rule to find the percentage of the values of a data set that lie within one standard deviation the mean.

How to apply the empirical rule

Suppose the mean is 89 and the standard deviation is 14. Determine the approximate percentage of values that lie within 47 and 131 of the mean.

The key to solving this problem is to find how many standard deviations 47 and 131 are of the mean.

In other words, we are just looking for k.

My strategy is to put the mean or 89 in the middle, 47 on the left side of the mean, and 131 on the right side of the mean.

47  ------------------ 89 ----------------- 131

Do you recall that in the lesson about Chebyshev's theorem, we showed that the distance between 89 and 131 is equal to kσ

kσ = 131 - 89

kσ = 42

Substitute 14 for σ.

We get:

k × 14 = 42

Divide both sides by 14.

We get k = 3.

About 99.7% of all the values lie within 47 and 131.