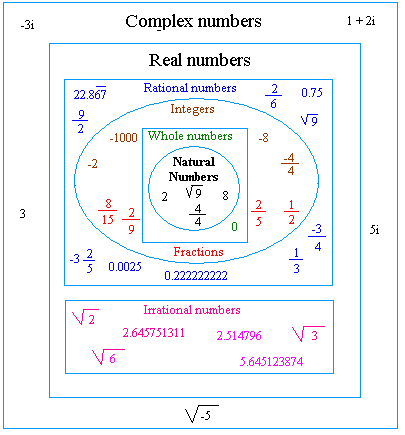
Classification of Numbers

In the chart below, are the classification of numbers. The chart will make things crystal clear. Study it carefully and then see below some important definitions and observations you need to make from the chart. Take the quiz below to see how much you know.

Chart Showing the Different Types of Numbers

Some Important Definitions and Observations about the Classification of Numbers

Natural Numbers

The natural numbers, also called positive integers, are the counting numbers 1, 2, 3, 4, 5, 6, ... 

The symbol that we use to represent the counting numbers is ℕ or N.

Observation #1:

Notice that it is OK to say that √(9) is also a natural number although it does not look like it. It is because √(9) = 3. √(9) is just another way to write the number 3.

The natural numbers can be further broken down into prime numbers and composite numbers.

For example, 5 is a prime number, but 12 is a composite number.

Whole Numbers

The whole numbers are the numbers 0, 1, 2, 3, 4, 5, 6, ...

The symbol that we use to represent the whole numbers is W.

Observation #2:

Notice that the only difference between the natural numbers and the whole numbers is the zero.

Whole numbers = natural numbers and the number zero

The whole numbers can be further broken down into prime numbers and composite numbers.

For example, 7 is a prime number, but 14 is a composite number.

Integers

The integers are the numbers ...,-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, ...

The symbol that we use to represent the integers is ℤ or Z.

Observation #3:

Notice that the difference between whole numbers and integers are the negative numbers.

Integers = whole numbers and the negative of the whole numbers.

The negative of the whole numbers (... -6, -5, -4, -3, -2, -1) are called negative integers and the positive of the whole numbers (1, 2, 3, 4, 5, 6, ...) are also called positive integers. Zero (0) is neither positive nor negative. 

The integers can be further broken down into even numbers and odd numbers. 

Example:

4 and -4 are even numbers. 5 and -5 are odd numbers.

Fractions

Fractions are numbers than can be expressed in the form a/b, in which a and b are whole numbers and b is not equal to zero. Examples of fractions are 1/2, 4, 1/3, 1, 12, 15/5, and 5/3.

A fraction can be written as a terminating decimal or as a non-terminating repeating decimal.

Example:

In decimal form, 1/2 = 0.5 and 0.5 is a terminating decimal. In decimal form, 1/3 = 0.3333333 and 0.3333333 is a non-terminating repeating decimal.

Observation #4:

All integers are fractions. Not all fractions are integers.

Example:

16 is an integer and can be written as 16/1 to make it a fraction.

However, 1/3 = -0.333333333 is not an integer.

Rational Numbers

Rational numbers are numbers that can be written in the form p/q, in which p and q can be integers and the denominator q is not equal to zero. Examples of rational numbers are 1/2, 4, -1/3, 1, 12, -15/4, 5/3, ...

The symbol that we use to represent the rational numbers is ℚ or Q.

Observation #5:

Rational numbers = Integers and fractions

A fraction is a rational number. However, a rational number may not be a fraction.

For example, 4/5 is both a fraction and a rational number. However, -4/5 is a rational number, but not a fraction. A fraction cannot have a negative sign. Once you put a negative sign next to a fraction, you must call it a rational number.

Irrational Numbers

Irrational numbers are numbers that cannot be written as common fractions or as a rational number.

The symbol that we use to represent the irrational numbers is P.

Examples of irrational numbers are √(7), √(3), 2.224879566117426874, and pi that is equal to 3.14...

Another way to see them is that they are neither repeating decimals nor terminating decimals. Irrational numbers are non-terminating, non-repeating decimals.

Observation #6:

Notice that √(16) is not an irrational number since √(16) is equal to 4. A square root sign does not mean it is always irrational.

Real Numbers

When you put together the set of rational numbers and the set of irrational numbers, you get the set of real numbers.

Real numbers = rational numbers and irrational numbers

The symbol that we use to represent the rational numbers is ℝ or R.

Examples of real numbers are 3, 1/4, -8, √(2), 5.47853997521, 2/3, 4.666666666, 0.8, 30.15, and (5.2)/6

Observation #7:

Why are real numbers called "real"? Because some numbers are not real. For example, negative infinity (-∞)  and positive infinity (∞) are not real numbers. The square root of a negative number such as √(-1) is not a real number either.

Complex Numbers

Complex numbers are numbers that can be written in the form a + bi, in which a and b are real numbers. a is called the real part and b is called the imaginary part.

By definition √(-1) is equal to i

The difference between complex numbers and real numbers is that complex numbers give solutions for the following expressions and more!

√(-1), √(-7), √(1-8), √(-25) = 5i, etc...

The symbol that we use to represent the complex numbers is ℂ.

Observation #8:

Notice that in our chart above, we included 3 as a complex number. This could happen if the imaginary part or b is equal to zero. On the other hand, if a is equal to zero, and b is not, you are dealing with imaginary numbers. For example, i, -2i, and (3/2)i are imaginary numbers.