Constructing an isosceles triangle

Constructing an isosceles triangle also known as drawing an isosceles triangle using only a straightedge and a compass is what I will show you here.

Step #1:

Take your ruler and a pencil and construct a segment of any length on a piece of paper as shown below.



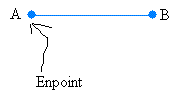
Then, you will open or close your compass opening to a distance bigger or smaller than segment AB.

Take your compass. Make your sure that the pencil is included in it. You may have to put one hand where the needle is and one hand where the pencil is in order to open or close the compass.

Then open or close the compass making sure that the distance of the opening is bigger or smaller than the length of segment AB.

For this situation, we will open the compass to a distance greater than segment AB.
Step #2:

Put the needle of your compass at A and draw an arc.



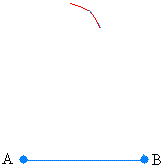
Put the needle of your compass at B and draw an arc.



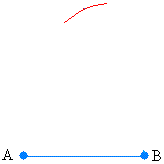
The two arcs should meet as shown below:




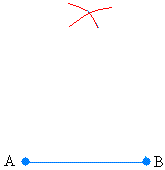
Step #3:

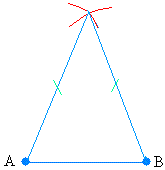
Draw the segments from the two endpoints to the point where the two arcs intersect.

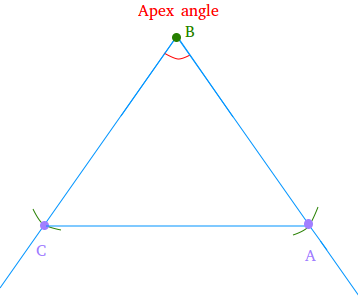
Constructing an isosceles triangle when the apex angle and the lengths of the two equal sides are given.

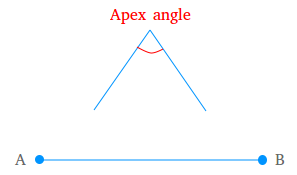
This construction is also straightforward and easy to do. The length of segment AB that you see above will be used for the two equal sides. In an isosceles triangle, the base angles are equal. The apex angle is the angle that is not equal to the base angles.

Here are the steps to follow to construct this isosceles triangle using the length of segment AB and the apex angle.

Step #1:

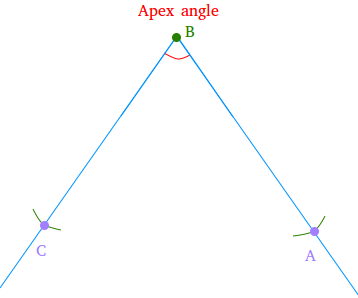
Using a straightedge, extend the sides of the apex angle so we can easily copy the length of segment AB.

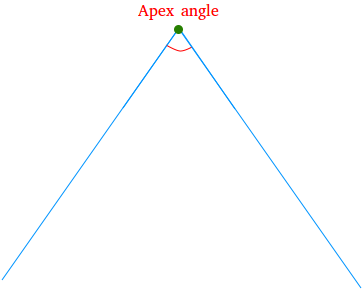
Step #2:

Using your compass, measure the length of segment AB. Then, keeping the opening of the compass the same, put the needle of the compass at the green dot or point B and draw arcs that intersect both sides of the angle. Call these points of intersection A and C.

Step #3:

Using your straightedge, draw a segment between A and C. Triangle ABC is an isosceles triangle!