Converse of the Pythagorean theorem
The converse of the Pythagorean theorem helps you to find out if a triangle is a right triangle. Furthermore, it can help you find the type of triangle you are dealing with.
Basically, the converse of the Pythagorean theorem states that whenever the sum of the squares of two sides (legs) equal to the square of the third side (hypotenuse) of the triangle, the triangle is a right triangle.
Suppose a, b, and c are sides of a triangle and c is the longest side of the triangle.
If c2 = a2 + b2, then the triangle is a right triangle. The triangle has 1 right angle and 2 acute angles.
A few examples showing how to use the converse of the Pythagorean theorem in order to determine is a triangle is a right triangle.
For example, given the following 3 sides, is the triangle a right triangle?
4, 5, 3
You just need to ask yourself the following question:
Is 52 = 42 + 32 ?
52 = 25 and 42 + 32 = 16 + 9 = 25
Since 25 = 25, the triangle with sides 4, 5, and 3 is a right triangle.
Notice that c must be equal to 5 since c is always the biggest side. After that it does not really matter which number is b or c. You can choose either 4 or 3 to be b or a.
Example #2
Do the sides 6, 8, and 10 form a right triangle?
You just need to ask yourself the following question:
Is 102 = 62 + 82 ?
102 = 100 and 62 + 82 = 36 + 64 = 100
Since 100 = 100, the triangle is a right triangle.
More examples showing how to use the converse of the Pythagorean theorem:
Example #3
Do the sides 8, 12, and 14 form a right triangle?
You just need to ask yourself the following question:
Is 142 = 82 + 122 ?
142 = 196 and 82 + 122 = 64 + 144 = 208
Since 196 is not equal to 208, the triangle is not a right triangle.
Example #4
Do the sides 9, 12, and 15 form a right triangle?
You just need to ask yourself the following question:
Is 152 = 92 + 122 ?
152 = 255 and 122 + 92 = 144 + 81 = 225
Since 255 = 255, the triangle is a right triangle.
Here is a figure summarizing the converse of the Pythagorean theorem
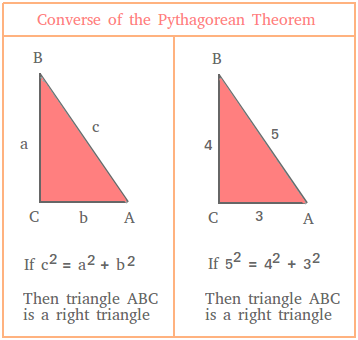
How to use the converse of the Pythagorean theorem
You can also use the converse of the Pythagorean theorem to find out if a triangle is an obtuse triangle or an acute triangle.
Obtuse triangle
If c2 > a2 + b2, then the triangle is an obtuse triangle.
If the square of the length of the longest side of a triangle is bigger than the sum of the squares of the lengths of the other two sides, then the triangle is obtuse. The triangle has 1 obtuse angle and 2 acute angles.
Acute triangle
If c2 < a2 + b2, then the triangle is an acute triangle.
If the square of the length of the longest side of a triangle is smaller than the sum of the squares of the lengths of the other two sides, then the triangle is acute. The triangle has 3 acute angles.
Example #5
Determine if the triangle with side lengths 12, 6, 8 is a right triangle, an obtuse triangle, or an acute triangle.
122 = 144
62 + 82 = 36 + 64
62 + 82 = 100
Since 144 is bigger than 100, the triangle is obtuse.
Example #6
Determine if the triangle with side lengths 5, 6, 7 is a right triangle, an obtuse triangle, or an acute triangle.
72 = 49
52 + 62 = 25 + 36
52 + 62 = 61
Since 49 is smaller than 61, the triangle is acute.
Buy a comprehensive geometric formulas ebook. All geometric formulas are explained with well selected word problems so you can master geometry.
