Converting repeating decimals to fractions

When converting repeating decimals to fractions, just follow the five steps below carefully.

Step 1:

Let x equal the repeating decimal you are trying to convert to a fraction.

Step 2:

Examine the repeating decimal to find the repeating digit(s).

Step 3:

Place the repeating digit(s) to the left of the decimal point.

Step 4:

Place the repeating digit(s) to the right of the decimal point.

Step 5:

Using the two equations you found in step 3 and step 4, subtract the left sides of the two equations. Then, subtract the right sides of the two equations

As you subtract, just make sure that the difference is positive for both sides.

Now let's practice converting repeating decimals to fractions with two good examples.

Example #1:

What rational number or fraction is equal to 0.55555555555

Step 1:

x = 0.5555555555

Step 2:

After examination, the repeating digit is 5.

Step 3:

To place the repeating digit ( 5 ) to the left of the decimal point, you need to move the decimal point 1 place to the right.

Technically, moving a decimal point one place to the right is done by multiplying the decimal number by 10.

When you multiply one side by a number, you have to multiply the other side by the same number to keep the equation balanced.

Thus, 10x = 5.555555555

Step 4:

Place the repeating digit(s) to the right of the decimal point.

Look at the equation in step 1 again. In this example, the repeating digit is already to the right, so there is nothing else to do.

x = 0.5555555555

Step 5:

Your two equations are:

10x = 5.555555555

   x = 0.5555555555

10x - x = 5.555555555 − 0.555555555555

9x = 5

Divide both sides by 9.

x = 5/9

Example #2:

What rational number or fraction is equal to 1.04242424242

Step 1:

x = 1.04242424242

Step 2:

After examination, the repeating digit is 42.

Step 3:

To place the repeating digit ( 42 ) to the left of the decimal point, you need to move the decimal point 3 places to the right.
Again, moving a decimal point three places to the right is done by multiplying the decimal number by 1000.

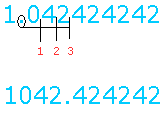
When you multiply one side by a number, you have to multiply the other side by the same number to keep the equation balanced

Thus, 1000x = 1042.42424242

Step 4:

Place the repeating digits to the right of the decimal point.

In this example, the repeating digit is not immediately to the right of the decimal point.

Look at the equation in step 1 one more time and you will see that there is a zero between the repeating digit and the decimal point.

To accomplish this, you have to move the decimal point 1 place to the right.

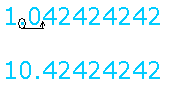
This is done by multiplying both sides by 10.

10x = 10.4242424242

Step 5:

Your two equations are:

1000x = 1042.42424242

   10x = 10.42424242

1000x - 10x = 1042.42424242 − 10.42424242

990x = 1032

Divide both sides by 990

x = 1032/990

To master this lesson about converting repeating decimals to fractions, you will need to study the two examples above carefully and practice with other examples.

Common pitfalls to avoid when converting repeating decimals to fractions

• Forgetting to put the decimal point right before the repeating digit(s).


• When subtracting the two equations, forgetting to subtract the smaller one from the bigger one.


• Not keeping good track of the number of places the decimal point was moved.


• Thinking that the repeating digit(s) is 8 if the decimal is 0.08