Cryptarithms
Cryptarithms are just math puzzles or math riddles. We can turn any regular addition, subtraction, multiplication, or division problem into a cryptarithm by replacing the numbers with letters.
Your job now is find the numerical values of these letters. In this lesson, I will show you, using my own techniques and thinking ability, how to solve cryptarithms.
Things to keep in mind!
You will experience some frustrations as you try to solve cryptarithms. This is a game involving trial and error. Therefore, give yourself plenty of time, keep trying, and do not get discouraged.
How to solve the cryptarithms below
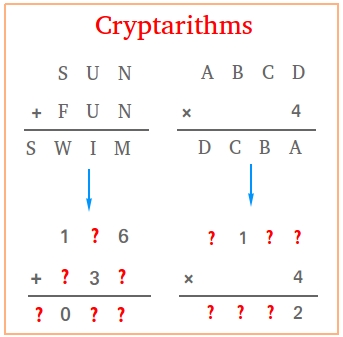
Example #1: Solve the cryptarithm below using only the numbers 0, 1, 2, 3, 6, 7, and 9. No letter can represent two different digits. For instance N cannot be 2 and 6 at the same time.
SUN
+ FUN
_____
SWIM
Guess and test is one of the strategies that we are going to use when solving cryptarithms. However, just guess and test is not enough when solving cryptarithms. You may need to make some good observations or use some basic math facts to solve cryptarithms in a timely fashion. Otherwise, we may end up guessing all day while trying to solve cryptarithms.
Solution to this cryptarithm
S U N
+ F U N
_____________
S W I M
Notice that N cannot be 0. When adding N and N, the result is M and M is different than N. However, 0 + 0 = 0, so you are not getting a different number. By the same token, U cannot be 0.
Notice also that N cannot be 2, 7, or 9 since 2 + 2 = 4, 7 + 7 = 14, and 9 + 9 = 18.
When adding, you will have to write down 4, or 8. However, 4 and 8 are not listed among the numbers we can use.
By the same token, U cannot be 2, 7 or 9. In sum, N and U can only be 0, 1, 3, or 6.
Notice that the following two additions are not possible.
2 appears twice
S 6 1
+ F 6 1
______________
S W 2 2
6 appears twice
S 6 3
+ F 6 3
______________
S W 2 6
For the one at the bottom, you could try to swap 3 and 6 and see what happens.
S 3 6
+ F 3 6
_______________
S W 7 2
We have 3 numbers left to use 0, 1, and 9. If you going to get a number with 4 digits as an answer, then 9 must be either S or F.
First possibility: S = 9 and F = 1
9 3 6
+ 1 3 6
_____________
1 0 7 2
Second possibility: S = 1 and F = 9
1 3 6
+ 9 3 6
_____________
1 0 7 2
The second possibility is of course our answer since this is the one that shows S in two locations. The other two additions below are more possibilities that would not have worked if we had tried them.
This combination does not work!
9 3 1
+ 7 3 1
______________
1 6 6 2
This combination does not work either!
9 1 3
+ 7 1 3
______________
1 6 2 6
Example #2: Find A, B, C, and D. The digits that we can pick from are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
ABCD
x 4
__________
DCBA
Solution to this cryptarithm
A B C D
x 4
_________________
D C B A
Important observation: The answer has 4 digits.
If the digit in red ( A ) is bigger than 2, the answer will have 5 digits instead 4. Therefore A cannot be 3, 4, 5, 6,7, 8, or 9. A can be either 1 or 2. This is the kind of logic you need to utilize when solving cryptarithms.
Suppose that A is 1 as shown below. Then, 4 times D = 1
1 B C D
x 4
_________________
D C B 1
4 times 1 = 4, 4 times 2 = 8, 4 times 3 = 12, 4 times 4 = 16, 4 times 5 = 20, 4 times 6 = 24, 4 times 7 = 28, 4 times 8 = 32, and 4 times 9 = 36
There are no numbers multiplied by 4 that will give you a 1 in the ones place. A cannot be 1 and since A cannot be 1, A must be 2.
2 B C D
x 4
______________
D C B 2
Only 4 times 3 or 4 times 8 will give you a 2 in the ones place, so D is 3 or 8.
First possibility
2 B C 3
x 4
________________
3 C B 2
Second possibility
2 B C 8
x 4
________________
8 C B 2
At this point, I feel more inclined to use the one at the bottom because 4 times 2 gives me the 8 that I want when I multiply 4 by 2. Again, be observant and use logic when solving cryptarithms!
2 B C 8
x 4
_______________
8 C B 2
My strategy now is to pick the right number for B. As I try to do this I notice that B cannot be bigger than 3. Anything bigger than 3 will have a carry that will force the 8 in the answer to be bigger. 2 is not a choice either since 2 cannot be repeated. My only choice for B then is 1.
2 1 C 8
x 4
_______________
8 C 1 2
When I do 4 times 8, I have a carry of 3.
4 times C + 3 must give a number with 1 in the tens place. My two choices for C are 2 and 7. 2 cannot be chosen since the 2 will be repeated. My only choice for C is 7.
2 1 7 8
x 4
________________
8 7 1 2
Some cryptarithms will be tougher than that to solve. However, you can eventually solve them by making some good observations.