Here is how to define locus in geometry
We can define locus in geometry as the set of all the points that satisfy given conditions. Notice that according to the definition, a locus is not a single point but a set of points.
To determine a locus, you will need to do the following two steps
- Use the condition given to draw points of the locus until you see a pattern.
- Connect the points and describe the locus fully.
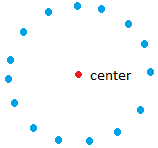
A great example of locus and we are all very familiar with it is the one resulting in a circle such as the circle shown in the figure above.
A circle is the locus of points at a given distance from a given point and whose center is the given point and whose radius is the given distance.
Define locus in geometry: some fundamental and important locus theorems
1) The locus of points equidistant from two given intersecting lines is the bisector of the angles formed by the lines.
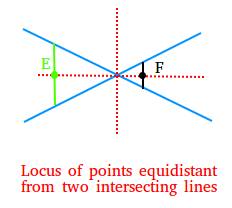
In the example above, we show the locus with red dashed lines. Notice the use of the green segment to show that there is a single point E on the locus that is equidistant from the intersecting lines. By the same token, for the black segment, there is a single point F on the locus that is equidistant from the intersecting lines.
2) The locus of all points equidistant from two given points A and B is the perpendicular of the line segment joining A and B.
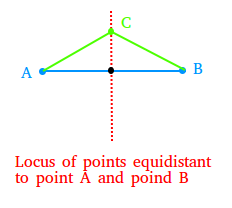
We show the locus of all points equidistant to points A and B with the red dashed line. We use two green segments to show where 1 single point or point C is equidistant to point A and B.
3) The locus of points equidistant from two given parallel lines is the line parallel to the two given lines and located between these given lines.

4) The locus of points equidistant from two concentric circles is the
circle concentric with the given circles and located midway between
them.
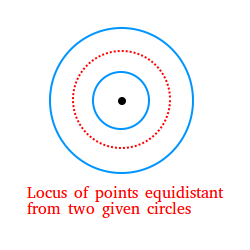
In our example immediately above, the locus is shown with the red dashed circle.
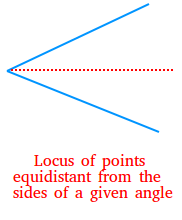
5) The locus of points equidistant from the sides of a given angle is the bisector of the angle.
This concludes our lesson about the definition of locus in geometry. If you did not quite understand something, please read the lesson again.