Definition of a Polynomial
Before giving you the definition of a polynomial, it is important to provide the definition of a monomial.
Definition of a monomial:A monomial is a variable, a real number, or a multiplication of one or more variables and a real number with whole-number exponents.
Examples of monomials and non-monomials
| Monomials |
9
|
x
|
9x
|
6xy
|
0.60x4y
|
| Not monomials |
y - 6
|
x-1 or 1/x
|
√(x) or x1/2
|
6 + x
|
a/x
|
Polynomial definition:
A polynomial is a monomial or the sum or difference of monomials. Each monomial is called a term of the polynomial.
Important observation!
Terms are separated by addition signs and subtraction signs, but never by multiplication signs.
- A polynomial with one term is called a monomial.
- A polynomial with two terms is called a binomial.
- A polynomial with three terms is called a trinomial.
Examples of polynomials:
| Polynomial |
Number of terms
|
Some examples
|
| Monomial |
1
|
2, x, 5x3
|
| Binomial |
2
|
2x + 5, x2 - x, x - 5
|
| Trinomial |
3
|
x2 + 5x + 6, x5 - 3x + 8
|
Similarity and difference between a monomial and a polynomial.:
A polynomial may have more than one variable.
For example, x + y and x2 + 5y + 6 are still polynomials although they have two different variables x and y.
By the same token, a monomial can have more than one variable. For example, 2 × x × y × z is a monomial.
A monomial will never have an addition or a subtraction sign.
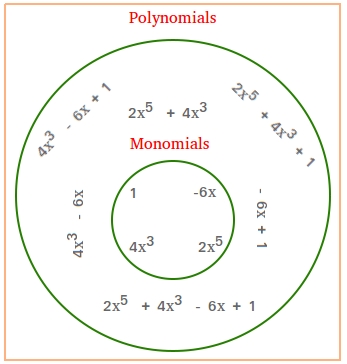
Take a close look at the Venn diagram below showing the difference between a monomial and a polynomial
For all expressions below, look for all expressions that are polynomials.
For those that are polynomials, state whether the polynomial is a monomial, a binomial, or a trinomial.
1) 3.4 + 3.4x
2) z2 + 5z-1 + 6
3) -8
4) 2c2 + 5b + 6
5) 14 + x
6) 5x - 2-1
7) 4 b2 - 2 b-2
8) f2 + 5f + 6
Answer: 1), 3), 4), 5), 6), and 8) are polynomials. 1), 5), and 6) are binomials. 3) is a monomial. 4) and 8) are trinomials.
2) and 7) are not because they have negative exponents
Notice that 6) is still a polynomial although it has a negative exponent. It is because it is the exponent of a real number, not a variable
In fact, 5x - 2-1 = 5x - 1/2 = 5x - 0.5
It is subtle, but if you have any questions about the definition of a polynomial, feel free to contact me.