Degree of a Polynomial
The degree of a polynomial is a very straightforward concept that is really not hard to understand.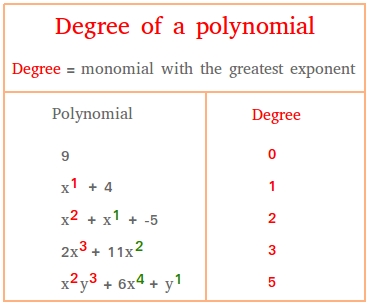
Recall that for y2, y is the base and 2 is the exponent.
More examples showing how to find the degree of a polynomial.
Example #1:
4x2 + 6x + 5
This polynomial has three terms. The first one is 4x2, the second is 6x, and the third is 5.
The exponent of the first term is 2.
The exponent of the second term is 1 because 6x = 6x1.
The exponent of the third term is 0 because 5 = 5x0.
What? 5x0 = 5?
Well, anything with an exponent of 0 is always equal to 1.
Thus, 5x0 = 5 × x0 = 5 × 1 = 5
Since the highest exponent is 2, the degree of 4x2 + 6x + 5 is 2.
Example #2:
2y6 + 1y5 + -3y4 + 7y3 + 9y2 + y + 6
This polynomial has seven terms. The first one is 2y2, the second is 1y5, the third is -3y4, the fourth is 7y3, the fifth is 9y2, the sixth is y, and the seventh is 6.
The exponent of the first term is 6.
The exponent of the second term is 5.
The exponent of the third term is 4.
The exponent of the fourth term is 3.
The exponent of the fifth term is 2.
The exponent of the sixth term is 1 because y = y1.
The exponent of the last term is 0 because 6 = 6x0.
Since the highest exponent is 6, the degree of 2y6 + 1y5 + -3y4 + 7y3 + 9y2 + y + 6 is 6.
Write a polynomial for the following descriptions
1)
A binomial in z with a degree of 10
2)
A trinomial in c with a degree of 4
3)
A binomial in y with a degree of 1
4)
A monomial in b with a degree of 3
Anwers:
1)
2z10 − 4
2)
c4 + c2 − 8
3)
y + 4
4)
b3
To find the degree of a polynomial or monomial with more than one variable for the same term, just add the exponents for each variable to get the degree.
Find the degree of x3y2 + x + 1.
The degree of this polynomial is the degree of the monomial x3y2
Since the degree of x3y2 is 3 + 2 = 5, the degree of x3y2 + x + 1 is 5