Difference of sets

This lesson will explain how to find the difference of sets. We will start with a definition.

Definition:

Given set A and set B the set difference of set B from set A is the set of all element in A, but not in B.

We can write A − B

Example #1.

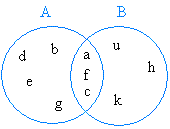
Take a close look at the figure above. Elements in A only are b, d, e, and g.

Therefore, A − B = { b, d, e, g}
Sometimes, instead of looking at the Venn Diagrams, it may be easier to write down the elements of both sets.

Then, we show in bold the elements that are in A, but not in B.

A = {b, d, e, g, a, f, c}

B = { k, h, u, a, f, c}


Example #2.

Let A = {1 orange, 1 pineapple, 1 banana, 1 apple}

Let B = {1 orange, 1 apricot, 1 pineapple, 1 banana, 1 mango, 1 apple, 1 kiwifruit }

Find B − A

Notice that this time you are looking for anything you see in B only

Elements that are in B only are shown in bold below.

B − A = {1 apricot, 1 mango, 1 kiwifruit}

Example #3.

Find A − B

B = { 1, 2, 4, 6}

A = {1, 2, 4, 6, 7, 8, 9 }

What I see in A that are not in B are 7, 8, and 9

A − B = { 7, 8, 9}

Example #4.

Find B − A

A = { x / x is a number bigger than 6 and smaller than 10}

B = { x / x is a positive number smaller than 15}

A = {7, 8, 9} and B = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}

Everything you see in bold above are in B only.

B − A = {1, 2, 3, 4, 5, 6, 10, 11, 12, 13, 14}

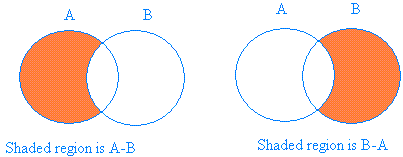
The graph below shows the shaded region for A − B and B − A
This ends the lesson about the difference of sets.

Difference of sets quiz to see how well you understand this lesson.