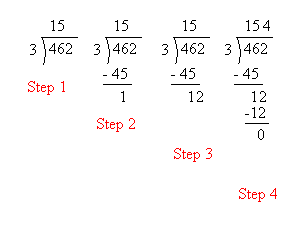Dividing whole numbers
This interactive long division tutor transforms the traditional process of dividing whole numbers into an engaging learning experience. Unlike standard calculators, it breaks down each step of long division, guiding students through the process of finding quotients, products, and remainders.
Interactive Long Division Tutor
Watch your division skills grow as you solve problems and get instant feedback on your answers. Perfect for students who want to build confidence in mathematics, or anyone looking to refresh their division skills. The clear, step-by-step approach takes the mystery out of long division, turning what can be a challenging process into an achievable and even enjoyable learning experience!
What is Long Divison?
Dividing whole numbers is the opposite of multiplying whole numbers. It is the process by which we try to find out how many times a number (divisor) is contained in another number (dividend). The answer in the division problem is called a quotient. In the division problem above ( 63 ÷ 7) , 7 is contained into 63, 9 times. (9 × 7 = 63)

Some other interesting examples showing how dividing whole numbers work.

When the dividend is bigger than 100, the answer may not be obvious. In this case you need to do long division in order to find the quotient. Study the following example (462 ÷ 3) carefully.
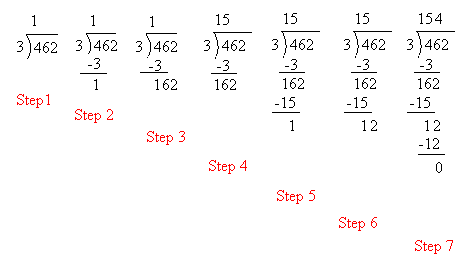
Here is a detailed explanation of step 1 to step 7 that may help you better understand this long division.
It is not easy to see immediately how many times 3 is contained into 462. It may not be easy also to see how many times 3 is contained into 46. However, it is fairly easy to see that 3 is contained into 4 once.Therefore, we do this in step 1 and put the 1 above the 4.
In step 2, we multiply 1 by 3 and subtract the answer or 3 from 4.
In step 3, we bring down the 62. Now, we need to find out how many times 3 is contained in 162. Still, it may not be obvious, so we will try to find out instead how many times 3 is contained into 16.
This is done in step 4 and we see that 3 is contained into 16 five times. We put the 5 above the 4.
In step 5 , we multiply 5 by 3 and subtract the answer or 15 from 16.
In step 6 , we bring down the 2.
In step 7 , we try to find out how many times 3 is contained into 12.
3 × 4 = 12, so 3 is contained into 12 four times.
Finally, we put the 4 above the 6.
The answer is 154. We can also say that 3 is contained into 462 one hundred fifty-four times.
Notice that the same division can be done faster if you can find out how many times 3 is contained into 46. 46 contains 3 fifteen times. Then, you can finish the problem in 4 steps as shown below: