Electric charge
Before showing you what an electric charge is, a discussion of what
electrical forces are is important. Keep reading carefully! In the end,
you will know why your finger received an electric shock when you touch a door handle.
Beside the force of gravity acting on you, imagine also another pair of forces that are very powerful acting on you called electrical attracting force and electrical repelling force.
See the electrical attracting force as coming from the earth and the electrical repelling force as coming from your body.
Why don't you feel the effect of this pair of forces? You don't feel anything because the two forces balance each other.
In the end, you only feel the force of gravity.
Now that you are aware of the presence of electrical forces, where does these force come from?
Electrical forces come from particles in atoms. Particles in atoms are called electrons, protons, and neutrons.
The model of an oxygen atom is shown below.
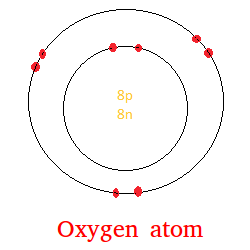
In an oxygen atom, there are 8 protons, 8 neutrons, and 8 electrons.
The 8 protons and 8 neutrons form what we call the nucleus.
The nucleus is surrounded by electrons and the electrons are shown in red.
Although
it is not clearly shown on the picture above, the mass of a proton is
far greater than that of an electron. The mass of a proton is almost
2000 times the mass of an electrons.
It is commonly
accepted that an electron carries a negative charge and a proton carries
a positive charge. The charge of an electron is equal in magnitude to
the charge of an electron.
The protons attract the electrons and hold them in orbit. However, electrons repel other electrons.
Basically, opposite charges attract, but like charges repel.
Under normal condition, there are as many electrons as protons in an atom. we say that the atom has a zero net charge.
If an atom happens to have more electrons or more protons, we call this phenomenon charge or electric charge.
If the number of electrons exceeds the number of protons, the atom is negatively charged.
On the other hand, If the number of protons exceeds the number of electrons, the atom is positively charged.
Conservation of electric charge
A neutral atom is an atom that has the same number of electrons as protons.
In the atom shown above, the 2 innermost negatively electrons are attracted a lot to the positively charged nucleus. However, it is not the same of the other 6 outermost electrons. They can easily be cut loose by outside forces.
If an electron is removed or lost, the atom is no longer neutral, it is electrically charged.
Rubber
does not easily lose its electrons while this happen a lot easier with
silk or human skin. We say that rubber has more electron affinity.
- So if you rub silk against rubber, the rubber will gain the electrons lost by the silk.
- If you brush electrons onto your feet while walking across a rug, you will be become negatively charged.
- If you become negatively charged and then touch a door handle with your finger, you may sometimes experience a small electric shock.
This happened because your body was not neutral, but negatively charged and the door handle was positively charged with less electrons.
The door handle wanted the extra electron(s) from your body.
As the extra electrons transferred from your body to the door handle, you experienced a tiny shock. This is an example of static electricity or electricity at rest since no wires are involved here.
It is important to note that electrons are neither created nor destroyed. Instead, they are just transferred from one material to another. This is the principle of conservation of charge.
When an atom is electrically charged, the atom has a net charge. An atom
that is electrically charged is called an ion. A positive ion has a net
positive charge while a negative ion has a net negative charge.
Whenever objects carry a net positive or negative charge, there is an
imbalance in electrical charge. As a result, electrical forces will
arise that will either cause objects with this imbalance to either
attract or repulse each other.
Electric charge quiz
This electric charge quiz will test your knowledge of electrical force and charge.
After completing this quiz, you should be able to clearly see the difference between electrical force and electrical charge. You will also know how an electric charge is created. You will not need to use a paper and pencil to complete this quiz.
First, read the lesson here about electric charge and then take this quiz.
Objective of the quiz:
- Understand the meaning of electrical charge
- Understand the meaning of electrical force
- Know where electrical forces come from
- Know what particles are
- Understand how the conservation of electric charge works.
- Understand what the nucleus is
- Understand what static electricity is
- Know what a net charge is
|
Test your knowledge with the quiz below: |