Equation of a circle
The standard equation of a circle, also called the standard form, is (x - h)2 + (y - k)2 = r2. The radius of the circle is r, the center of the circle is (h , k), and (x , y) is any point on the circle.
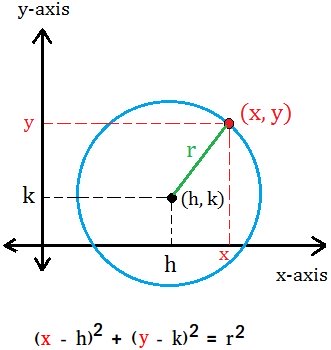
How to write the equation of a circle using the coordinates of the center of the circle and the radius of the circle
Example #1
Write the standard equation of the circle with center (6, -4) and radius 5.
The standard form is (x - h)2 + (y - k)2 = r2
Substitute 6 for h, -4 for k, and 5 for r in the standard form.
(x - 6)2 + [y - (-4)]2 = 52
Simplify the equation
(x - 6)2 + (y + 4)2 = 25
Example #2
Write the standard equation of the circle with center (3, -1) that passes through the point (2,2).
The length of the radius is the distance between the center and the point on the circle. Use the distance formula to find the radius.
r = √[(x - h)2 + (y - k)2]
r = √[(2 - 3)2 + (2 - -1)2]
r = √[(-1)2 + (3)2]
r = √[1 + 9]
r = √(10)
The standard form is (x - h)2 + (y - k)2 = r2
Substitute 3 for h, -1 for k, and √(10) for r in the standard form.
(x - 3)2 + [y - (-1)]2 = [√(10)]2
Simplify the equation
(x - 3)2 + (y + 1)2 = 10
How to find the center and the radius of the circle using the standard form
Example #3
Suppose (x - 2)2 + (y + 3)2 = 42 is an equation of a circle. Find the radius and the center of this circle.
Just compare (x - 2)2 + (y + 3)2 = 42 with (x - h)2 + (y - k)2 = r2
It might not be difficult to see immediately that r = 4. However, to find h and k, we can solve the two equations x - h = x - 2 and y - k = y + 3.
x - h = x - 2
x - x - h = x - x - 2
-h = -2
Multiply both sides by -1
(-1)(-h) = (-1)(-2)
h = 2
y - k = y + 3
y - y - k = y - y + 3
-k = +3
Multiply both sides by -1
(-1)(-k) = (-1)(+3)
k = -3
The circle is located at (2 , -3) on the coordinate system and the radius is 4.
How to derive the standard form of an equation of a circle.
Start with the circle you see below. Then put the circle on the coordinate system.
Finally, label the circle to show the center and a point on the circle. Recall that (h, k) is the center of the circle and (x, y) is a point on the circle. The distance between (h, k) and (x, y) is the length of the radius.
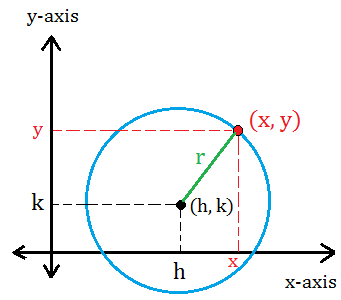
To find the equation, we just need to use the distance formula which can be used to find the distance between two points.
| __________________ | |
| Distance formula = √ | (x1 - x2)2 + (y1 - y2)2 |
| __________________ | |
| d = √ | (x1 - x2)2 + (y1 - y2)2 |
Notice that the distance between (h,k) and (x,y) is r. Thus d = r
| __________________ | |
| r = √ | (x1 - x2)2 + (y1 - y2)2 |
Let (x1, y1) = (x,y) and (x2, y2) = (h,k)
| __________________ | |
| r = √ | (x - h)2 + (y - k)2 |
Square each side of the equation
r2 = ( x - h )2 + ( y - k )2
Besides the standard form, there are three different forms that can be used to represent the equation of a circle.
- "General form"
- Parametric form
- Polar form
"General form" of the equation of a circle
The general form of the equation of a circle is x2 + y2 + Dx + Ey + F = 0, where D, E, and F are constants and real numbers.
You can find the general form of the equation of a circle by expanding the standard form.
For example, expand (x - 2)2 + (y + 3)2 = 42 to write it in general form.
x2 - 4x + 4 + y2 + 6y + 9 = 16
Combine like terms
x2 - 4x + y2 + 6y + 4 + 9 = 16
x2 - 4x + y2 + 6y + 13 = 16
Subtract 16 from both sides of the equation
x2 - 4x + y2 + 6y + 13 - 16 = 16 - 16
x2 - 4x + y2 + 6y + -3 = 0
x2 + y2 - 4x + 6y - 3 = 0 is the "general form" of (x - 2)2 + (y + 3)2 = 42
Parametric equations of a circle
Draw a circle as shown below on the Cartesian plane. Let P with x and y coordinates be any arbitrary point on the circle. Using two of the six basic trigonometric functions, write expressions for sinθ and cosθ.
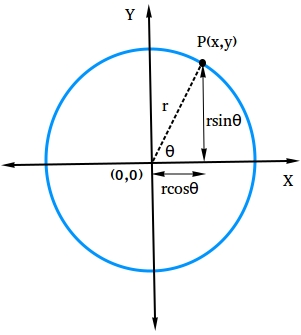
cos θ = x/r
sin θ = y/r
Multiply both sides of the two equations above by r to solve for x and y.
We get x = r cos θ and y = r sin θ
Suppose (0,0) is the center of a circle. The variable θ is called a parameter and the equations x = r cos θ and y = r sin θ are called parametric equations for the circle.
Suppose the centre of the circle is not located at (0, 0) but at (h, k)
In this case, simply add h to the x-coordinate and k to the y-coordinate.
If (h, k) is the center of the circle, then the parametric equations for the circle are
x = h + r cos θ and y = k + r sin θ
Polar form of a circle
It is quite easy and straightforward to find the polar form of a circle by using the standard equation of a circle whose center is at the origin and the parametric equations of a circle whose center is also at the origin.
Suppose k is the radius of a circle in the coordinate system. We find the polar form by substituting r cos θ for x and r sin θ for y in x2 + y2 = k2
(r cos θ)2 + (r sin θ)2 = k2
r2 cos2 θ + r2 sin2 θ = k2
r2 (cos2 θ + sin2 θ) = k2
r2 (1) = k2
r2 = k2
r = ±k