Factoring Integers
Step-by-Step Integer Factorization
Step 1: Start with a Number
Let's begin by choosing a number to factor:
Step 2: Find the Smallest Factor
What's the smallest number that divides into this number evenly?
Steps taken:
Quiz Mode
Enter the prime factorization (use x as multiplication symbol):
How to Factor Integers
Factoring integers is the easiest thing we can factor. It means to make the integer look like a multiplication problem by looking for its prime factorization. In other words, factor the integer until all factors are prime numbers.
It is very important to know how to do this before learning how to find the greatest common factor and how to factor trinomials.
Here is the algorithm:
When factoring, start by dividing the number by 2. Then, keep dividing any factor divisible by 2 that is not prime by 2 until no factors are divisible by 2.
When no factors are divisible by 2, start by dividing by 3 until no factors are
divisible by 3.
When no factors are divisible by 3, start by dividing by 4 until.....
and so forth...
Factoring Integers with a Couple of Example.
Example #1
Factor 4
Dividing 4 by 2 gives 2, so
4 = 2 * 2
Example #2
Factor 12
Dividing 12 by 2 gives 6, so
12 = 2 * 6
However, 6 is a factor divisible by 2, so factor 6.
Factoring 6 gives 2 * 3
Putting it all together,
12 = 2 * 6 = 2 * 2 * 3
When factoring integers a problem can get complicated when the number is big. when this happens make a tree as the following example demonstrates. We call this a factor tree.
Factor 72
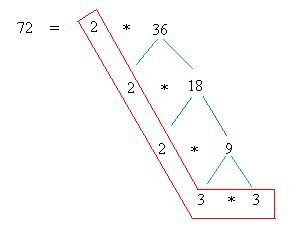
Pulling out all factors inside the red shape that looks like a golf bat, we get:
72 = 2 * 2 * 2 * 3 * 3
Example #4
Factor 240

Once again, pulling out all factors inside the red shape that looks like a golf bat, we get:
240 = 2 * 2 * 2 * 2 * 3 * 5
You should notice tough that 72 and 240 can be factored faster than that if you know very well your multiplication table.
72 = 8 * 9
8 = 2 * 2 * 2 and 9 = 3 * 3
So, 72 = 2 * 2 * 2 * 3 * 3
240 = 24 * 10
10 = 2 * 5 and 24 = 4 * 6 = 2 * 2 * 2 * 3
So, 240 = 2 * 2 * 2 * 2 * 3 * 5