Factoring using the box method

Factoring using the box method is probably the best way to factor a trinomial of the form ax² + bx + c.

The box is just a 2x2 square that we use to put the terms of the trinomial.

Example #1

Factor 2x² + 9x + 10 using the box method.

Step 1

First, put 2x² and 10 in the box below as shown. You will always put the first term in the first row and the first column and the last term in the second row and second column.

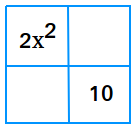
Step 2

Multiply the first term by the last term: 2x² ×10 = 20x²

Look for factors of 20x² that will add up to the second term or 9x.

20x²    =  1x  × 20x
20x²  = 2x × 10x
20x²   = 4x × 5x

Since 4x and 5x add up to 9x, put 4x and 5x in the box.

Step 3

Find the greatest common factor of each row and write them down on the left or right side of the box. Then, find the greatest common factor of each column and write them down on top or at the bottom of the box.

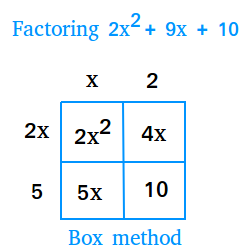
Notice the following:

2x times x = 2x²
2x times 2 = 4x
5 times x = 5x
5 times 2 = 10

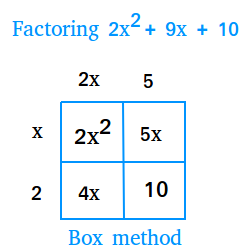
The factors are (2x + 5)  and (x + 2), so 2x² + 9x + 10 = (2x + 5) ×  (x + 2)

4x and 5x are interchangeable, so you could put 5x in the first row and 4x in the second row and still get the same answer.

A common pitfall to avoid when factoring using the box method.

When factoring using the box method, you need to make sure that the greatest common factor of a, b, and c in ax² + bx + c is equal to 1 as example #2 shows.

Example #2

Factor 6x² + 27x + 30 using the box method.

Step 1

First put 6x² and 30 in the box below as shown.

Step 2

Multiply the first term by the last term: 6x² × 30 = 180x²

Look for factors of 180x² that will add up to 27x.

Since 12x × 15x = 180x² and 12x + 15x = 27x, put 12x and 15x in the box.

Step 3

Find the greatest common factor of each row and write them down on the left or right side of the box. Then, find the greatest common factor of each column and write them down on top or at the bottom of the box. We end up with the following box.

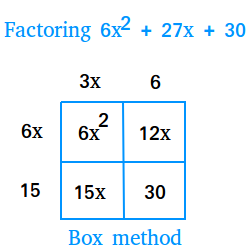
However, we have a little problem . 6x times 3x is not equal to 6x², 6x times 6 is not equal to 12x, 15 times 3x is not equal to 15x, and 15 times 6 is not equal to 30.

In order for us to see what happened here, we need to make an important observation.

Notice that 6x² + 27x + 30 = 3(2x² + 9x + 10 ) and we already factored 2x² + 9x + 10

2x² + 9x + 10 =  (2x + 5)× (x + 2)

Therefore, 6x² + 27x + 30 = 3(2x² + 9x + 10 ) = 3(2x + 5)×(x + 2)

Looking at the box immediately above again, we see that we can factor the entire thing by 3. And if we do that we will get the same answer as illustrated below.

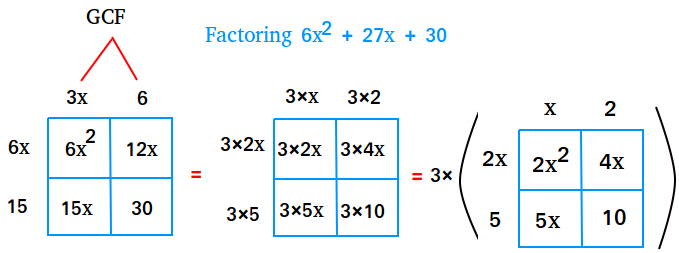
Look at the image immediately above again. The box inside the parentheses is the box that we used to factor 2x² + 9x + 10.

Therefore when factoring using the box method, make sure you factor the trinomial ax² + bx + c until the greatest common factor of a, b, and c is equal to 1 to avoid complicating things.

Example #3

Factor 4x² - 8x - 12 using the box method.

First, factor 4x² - 8x - 12 using the greatest common factor.

4x² - 8x - 12 = 4(x² - 2x - 3)

Now, you just need to factor x² - 2x - 3 using the box method

Step 1

First put x² and -3 in the box

Step 2

Multiply the first term by the last term: x² × -3 = -3x²

Look for factors of -3x² that will add up to -2x.

Since -3x × x = -3x² and -3x + x = -2x put -3x and x in the box.

Step 3

Find the greatest common factor of each row and write them down on the left or right side of the box. Then, find the greatest common factor of each column and write them down on top or at the bottom of the box. We end up with the following box.

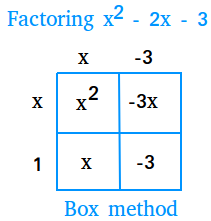
x² - 2x - 3 = (x + 1)(x - 3)

4x² - 8x - 12 = 4(x² - 2x - 3) = 4(x + 1)(x - 3)