How to factor a trinomial by getting rid of the impostor
Learn how to factor a trinomial of the form ax2 + bx + c when a is not equal to 1 by getting rid of the "impostor".
The impostor here is the leading coefficient a or the coefficient of ax2. In order to use this method, GCF(a,b,c) = 1 (The greatest common factor of a, b, and c must equal to 1). The impostor will show itself in the factored form as shown below.
a( )( ) or b( )c( ) if a = bc
This method is straightforward and does not involve too much trial and error and that is why I like it. The best way to understand what we mean by "getting rid of the impostor" or "a" is to solve some examples.
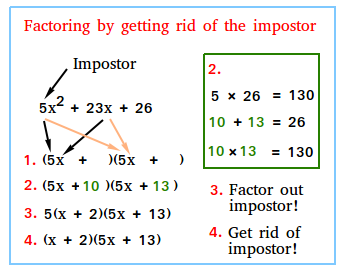
First, read the example in the figure above carefully. It is OK if you do not understand everything just yet! Then, read the 3 examples below showing how to factor a trinomial quickly and efficiently by getting rid of the impostor.
More examples showing how to factor a trinomial by getting rid of the impostor
Example 1: 3x2 + 7x + 2
For this example, the impostor that we will eventually get rid of is 3.
Step 1
Factor any GCF if any. Since 3x2 + 7x + 2 does not have any GCF, go to step 2.
Step 2
Multiply the coefficient of the leading term by the constant term (a × c) and then find factors of the product that add up to the coefficient of the second term or 7.
a × c = 3 × 2 = 6
Step 3
Factor as if a = 1 using (3x + blank)(3x + blank) as your factored form. Then, ask what multiplies to 6 and adds up to 7.
Notice that the factored form is the product of two binomials. Notice also how we used 3x as the first term in each factor or binomial! This is the way to do it every time in this step when factoring by getting rid of the impostor.
Since 1 × 6 = 6 and 1 + 6 = 7, use 1 and 6 to fill in the blank.
We get (3x + 1)(3x + 6)
Step 4
Pull out impostor by GCF and banish. In other words, using (3x + 1)(3x + 6), factor out the GCF for each factor.
(3x + 1)(3x + 6) = (3x + 1)×3(x + 2)
As you can see, the impostor is the 3, so banish it.
After banishing or getting rid of the impostor which is 3, the final answer is (3x + 1)(x + 2)
Example 2: 8x2 - 10x - 3
For this example, the impostor that we will eventually get rid of is 8.
Step 1
Factor any GCF if any. Since 8x2 - 10x - 3 does not have any GCF, go to step 2.
Step 2
Multiply a by c and then find factors of the product that add up to -10.
a × c = 8 × -3 = -24
Step 3
Factor as if a = 1 using (8x + blank)(8x + blank) as your factored form. Then, ask what multiplies to -24 and adds up to -10.
Notice again how we used 8x as the first terms of the binomials!
Since -12 × 2 = -24 and -12 + 2 = -10, use -12 and 2 to fill in the blank.
We get (8x + -12)(8x + 2)
Step 4
Pull out impostor by GCF and banish. In other words, using (8x + -12)(8x + 2), factor out the GCF for each factor.
(8x + -12)(8x + 2) = 4(2x + -3)×2(4x + 1)
As you can see, the impostor is split up into two of its factors, so banish it by multiplying the two numbers to get your real impostor, 8.
After banishing or getting rid of the impostor which is 8, the final answer is
(2x + -3)(4x + 1)
How to factor a trinomial by getting rid of the impostor when there is a GCF in step 1
Example 3: 6x2 + 8x + 2
Step 1
Factor the GCF if any. GCF = 2, so 6x2 + 8x + 2 = 2(3x2 + 4x + 1 )
Step 2
Be careful here! The impostor is 3 since we need to factor 3x2 + 4x + 1.
Multiply a by c and then find factors of the product that add up to 4.
a × c = 3 × 1 = 3
Step 3
Factor as if a = 1 using (3x + blank)(3x + blank) as your factored form. Then, ask what multiplies to 3 and adds up to 4.
Since 3 × 1 = 3 and 3 + 1 = 4, use 3 and 1 to fill in the blank.
We get (3x + 1)(3x + 3)
Step 4
Pull out impostor by GCF and banish. In other words, using (3x + 1)(3x + 3), factor out the GCF for each factor.
(3x + 1)(3x + 3) = (3x + 1)×3(x + 1)
After banishing the impostor, we get (3x + 1)(x + 1)
However, do not forget the factor in step 1, so the final answer is 2(3x + 1)(x + 1)
How to factor trinomials by trial and error
You may need to factor by trial and error when the leading coefficient is not equal to 1. For example, you can solve 8x2 - 10x - 3 also by trial and error. This means that you have to write and try all possible combinations of the factored form of the trinomial and then use FOIL method to see which of these combinations will give back the trinomial.
The possible combinations of factored form can be found with the leading term 8x2 and the third term -3. The right combination is shown in blue.
(8x + 3)(x - 1)
(8x - 3)(x + 1)
(8x + 1)(x - 3)
(8x - 1)(x + 3)
(4x + 3)(2x - 1)
(4x - 3)(2x + 1)
(4x + 1)(2x - 3) = 8x2 - 12x + 2x - 3 = 8x2 - 10x - 3
(4x - 1)(2x + 3)
As you can see, factoring a trinomial by trial and error is boring and requires more patience to test all these combinations. This is why I love to factor by getting rid of the impostor.
How to factor trinomials when the leading coefficient is 1
For example, when factoring x2 + bx + c, there is no need to do trial and error.
Here is the shortcut to follow:
Put x in the first position of each binomial: (x + last position)(x + last position)
To find the terms that go in the last positions just look for all possible factors of the c term, that when added, will equal to the coefficient of the middle term.
Factor x2 + 7x + 12
The factors of 12 are 1 and 12, 2 and 6, and 3 and 4.
When you add 3 and 4, you get 7. Therefore, the last terms of the binomials are 3 and 4.
x2 + 7x + 12 = (x + 3)(x + 4)
Factor x2 + -6x - 27
The factors of -27 are -27 and 1, 27 and -1, -9 and 3, 9 and -3
When you add -9 and 3, you get -6. Therefore, the last terms of the binomials are -9 and 3.
x2 + -6x - 27 = (x - 9)(x + 3)
Since the b term is negative, the absolute value of the negative factor must be bigger than the absolute value of the positive factor. |-9| > |3|
How to factor a trinomial using the box method
How to factor a polynomial using a sum and difference of cubes
100 Tough Algebra Word Problems.
If you can solve these problems with no help, you must be a genius!
Recommended