How to find a reflection image
To find a reflection image of a point or a shape, there are some rules you can follow although it is not always possible to follow a rule.
First, let us start with all situations where you can just follow a rule to quickly find the location of the reflected image on the coordinate system.
Keep in mind that once you know how to find a reflection image for a point, you can easily find it for a shape. For example, if the shape has 3 points, just find the reflected image for all 3 points and then connect these points with a line.
How to find a reflection image using the x-axis or the y-axis
Reflection of a point across the x-axis
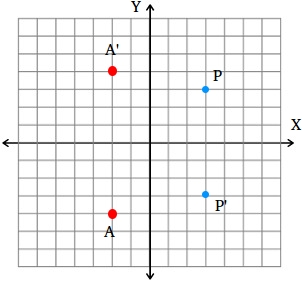
The coordinate of point P is (3, 3) and the coordinate of the reflected image P' is (3, -3)
The coordinate of point A is (-2, 4) and the coordinate of the reflected image A' is (-2, -4)
What do you notice about the x-coordinate and y-coordinate of the preimage and image?
We see that the x-coordinate of the preimage stays the same, but the y-coordinate of the image is the opposite of the y-coordinate of the preimage.
In general, when reflecting a point across the x-axis, if the coordinate of the preimage is (x , y), then the coordinate of the reflected image is (x , -y)
Reflection of a point across the y-axis
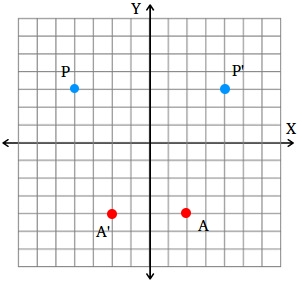
The coordinate of point P is (-4, 3) and the coordinate of the reflected image P' is (4, 3)
The coordinate of point A is (2, -4) and the coordinate of the reflected image A' is (-2, -4)
What do you notice about the x-coordinate and y-coordinate of the preimage and image?
We see that the y-coordinate of the preimage stays the same, but the x-coordinate of the image is the opposite of the x-coordinate of the preimage.
In general, when reflecting a point across the y-axis, if the coordinate of the preimage is (x , y), then the coordinate of the reflected image is (-x , y)
How to find a reflection image using the lines y = x and y = -x
Reflection of a point across the line y = x

The coordinate of point P is (1, 4) and the coordinate of the reflected image P' is (4, 1)
The coordinate of point A is (-5, -2) and the coordinate of the reflected image A' is (-2, -5)
Just swap the x-coordinate with the y-coordinate
In general, when reflecting a point across the line y = x, if the coordinate of the preimage is (x , y), then the coordinate of the reflected image is (y, x)
Reflection of a point across the line y = -x

The coordinate of point P is (2, 4) and the coordinate of the reflected image P' is (-4, -2)
The coordinate of point A is (4, -1) and the coordinate of the reflected image A' is (1, -4)
Therefore, swap the x-coordinate with the y-coordinate and then take the opposite of both coordinates.
In general, when reflecting a point across the line y = -x, if the coordinate of the preimage is (x , y), then the coordinate of the reflected image is (-y, -x)
Reflection of a point in the origin
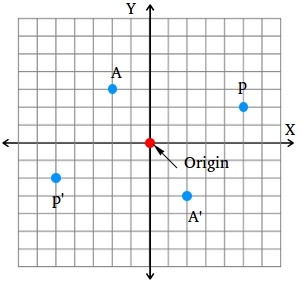
The coordinate of point P is (5, 2) and the coordinate of the reflected image P' is (-5, -2)
The coordinate of point A is (-2, 3) and the coordinate of the reflected image A' is (2, -3)
Just take the opposite of both coordinates.
In general, when reflecting a point in the origin, if the coordinate of the preimage is (x , y), then the coordinate of the reflected image is (-x, -y)
When reflecting a point across any line, just keep this mind. The distance between the point and the line and the reflected point and the line is exactly the same.
When reflecting a point A in any point P, just keep this mind these two things.
The distance between point A and point P and the reflected point A' and point P is exactly the same.
Point P, the reflected point A' and point A are colinear.