How to find a translation image
To find a translation image of a shape, you can use the following rule or formula.
Suppose you want to translate or slide point P a units horizontally and b units vertically. Then, change the x-values and y-values of the coordinates of P.
P = (x, y) translates to P' = (x + a, y + b)
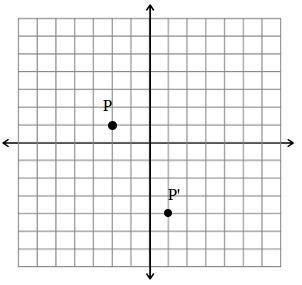
Find the image of point P (-2, 1) under the translation (x, y) →(x + 3, y - 5)
Under this translation, P (-2, 1) translates to (-2 + 3, 1 - 5) or P'(1, -4)
Example #2
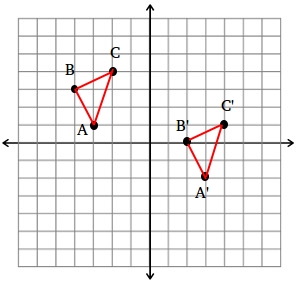
Find the image of triangle ABC under the translation (x, y) →(x + 6, y - 3)
The points of the triangle of are A(-3, 1), B(-4, 3), and C(-2, 4). Use the rule to find each vertex in the translated image.
A(-3, 1) translates to (-3 + 6, 1 - 3) or A'(3, -2)
A(-4, 3) translates to (-4 + 6, 3 - 3) or A'(2, 0)
A(-2, 4) translates to (-2 + 6, 4 - 3) or A'(4, 1)
Example #3
A translation maps (8, -12) → (0, 14). Find a rule to describe this translation.
(8, -12) → (0, 14)
We are looking for a and b such that the rule is (x + a, y + b). We know x = 8 and y = -12
Therefore, (0, 14) → (8 + a, -12 + b)
0 = 8 + a
a = -8
14 = -12 + b
b = 14 + 12 = 26
The rule is (x, y) → (x - 8, y + 26)
Example #4
The coordinate of the image of a point is (2, -5) under the translation (x , y) → (x - 2, y + 5). Find the coordinate of the preimage.
We are just looking for x and y and we know (2, -5) → (x - 2, y + 5)
2 = x - 2
x = 4
-5 = y + 5
y = -10
(x , y) = (4, -10)