Use counters to find the quotient and remainder

This lesson will show how to use counters to find the quotient and remainder. However, it is possible that you are not familiar with the meaning of the word counter.

What is a counter then? A counter is mostly used in elementary school. It could be a stone, a coin, or a chip. For example, to represent the number 7, students could be asked to show seven stones or seven chips.

Now let us see how we can find the quotient and the remainder using counters.

Example #1

27 divided by 4

Use 27 counters to represent the dividend 27 as shown below.

Now since you are dividing by 4, you will need to draw 4 big circles having the same amount of counters in each circle.

However, as you do this, you need to make sure that the number of counters left is less than 4.

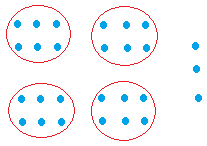
Notice that if you had put 5 counters in each circle, it would not be correct since there will be 7 counters left and 7 is bigger than 4.

There are 6 counters in each circle, so the quotient is 6.
There are 3 counters left over, so the remainder is 3

Example #2

30 divided by 8

Use 30 counters to represent the dividend 30 as shown below.

Again, since you are dividing by 8, you will need to draw 8 big circles having the same amount of counters in each circle.

However, as you do this, you need to make sure that the number of counters left is less than 8.

There are 3 counters in each circle, so the quotient is 3. There are 6 counters left over, so the remainder is 6.