Finger Multiplication
The use of finger multiplication has been widespread through the years. It is not the traditional way of doing multiplication in school today. However, if your kid has trouble remembering the whole multiplication table, multiplication with fingers is a good alternative!
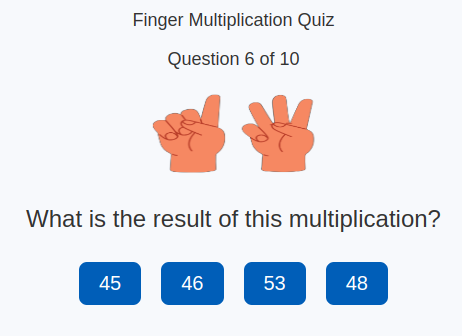
Finger Multiplication Quiz
To multiply with fingers, you are only required to remember the multiplication table up to 5 × 5. After that, all multiplication can be performed with your fingers.
Here is the technique
- The two numbers to be multiplied are each represented on a different hand
- Each hand may have some raised fingers and some closed fingers at the same time
- Number of fingers to raise = Factor − 5. Remember that a factor is a number in a multiplication problem
- The sum of the raised fingers is the number of tens
- The product of the closed fingers is the number of ones
A Few Examples Showing How to Do Finger Multiplication
Example #1: 7 × 8
For 7, use your left hand and raise 2 fingers (Factor − 5 = 7 − 5 = 2) . This means there are 3 closed fingers.
For 8, use your right hand and raise 3 fingers. This means that there are 2 closed fingers.
Sum of raised fingers = 2 + 3 = 5. This means we have 5 tens or 50.
Product of closed fingers = 3 × 2 = 6
This means that we have 6 ones.
50 + 6 = 56
Example #2: 9 × 6
For 9, use your right hand and raise 4 fingers. This means there is 1 closed finger.
For 6, use your left hand and raise 1 finger. This means that there are 4 closed fingers
Sum of raised fingers = 4 + 1 = 5. This means we have 5 tens or 50.
Product of closed fingers = 1 × 4 = 4
This means that we have 4 ones
50 + 4 = 54
Example #3: 8 × 5
For 8, use your left hand and raise 3 fingers. This means there are 2 closed fingers.
For 5, use your left hand and raise no finger. This means that there are 5 closed fingers.
Sum of raised fingers = 3 + 0 = 3.
This means we have 3 tens or 30
Product of closed fingers = 2 × 5 = 10
This means that we have 10 ones or 1 ten or 10
30 + 10 = 40