Free fall problems
These free fall problems will show you how to solve a variety of word
problems related to objects that are falling from a certain height.
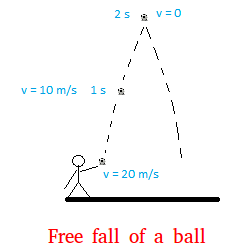
Problem #1: A ball is thrown straight up in the air as shown in the figure above. If it takes the ball 2 seconds to reach its maximum height, what is the initial velocity?
Solution
When in the air, the ball is under the influence of gravity.
On the way up, the speed of the ball will decrease by 10 m / s each second until it reaches a speed of 0 ( maximum height)
The initial speed must have been 20 m / s.
You could also use the equation v = v0 + g × t and v0 is the initial velocity.0 = v0 + 10 × 2
0 = v0 + 20
Since 0 = -20 + 20, v0 = -20
Why do we have a negative?
The equation v = v0 + g × t is missing something important.
The value g = 10 m / s 2 is missing an important math concept.
There should be a negative next to g
v = v0 + -g × t
0 = v0 + -10 × 2
0 = v0 + -20
Since 0 = 20 + -20, v0 = 20
The value of g is just a measurement. In math anything upward the y-axis is positive. Since the acceleration is downward the y-axis, it should really be -g instead of just g.
Whenever you are solving free fall problems, keep the aforementioned in mind.
Problem #2: What is the instantaneous speed of a book dropped from the twenty-fifth floor after 2.5 second?
Solution:The formula that gets you the instantaneous speed is v = g × t. Let us use g = 10 m / s2
t = 2.5 second
v = g × t = 10 m / s2 × 2.5 s
v = 25 m /s
Interesting free fall problems
Problem #3 :
How high is a building if it takes 5 seconds for a ball to hit the floor ?
Pretend the object was dropped from the rooftop and a man was holding the ball at a height of 1 meter before letting it go.Use g = 10 m / s2

Notice that when g = 10 m /s 2, we can simplify the formula to 5 × t2
|
g × t2
2
|
=
10 × t2
2
|
=
10
2
× t2
|
So, we can just use the formula above to simplify the problem.
d = 5 × 52d = 5 × 25
d = 125 meters.
However, the object was dropped from a height of 1 meter.
This is the height the man was holding the ball.
Therefore, subtract 1 from 125 to get the height of the building
h = 125 - 1 = 124.
The building is 124 meters.
This is a very interesting free fall problem because it give us another very efficient way to measure the height of a building.
Problem #4: Your turn to solve a free fall problem!
The world's tallest building is Burj Dubai. Rounded to the neatest 10, the building is 830 meters high. How long will it take an object to hit the floor?
Solve this free fall problem yourself. I will not solve it for you!