Friction on an inclined plane 

To show you how to calculate the friction on an inclined plane, we will use the diagram below. The diagram shows an object of mass m on an inclined plane.

After trial and error, we realize that if the angle is slightly higher than 30 degrees, the object will slide down the incline. However, when the angle is 30 degrees, the object is on the verge of sliding. 

When the object is on the verge of moving, what is the coefficient of static friction μ_s between the object and the surface the object is placed on?

First important concept when dealing with friction on an inclined plane

Identify the forces

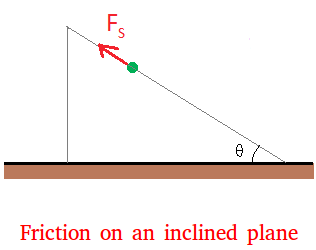
Since the object does not slide when the angle is 30 degrees, the force of friction is holding the object in place. It is usually directed opposite to the direction of movement. We show this force below but we use a green dot to represent the object to facilitate the reading. 

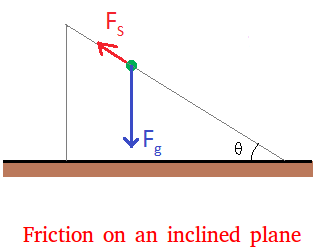
When the angle is greater than 30 degrees, the object slides down. What force causes the object to slide? It is the force of gravity since no hands are pushing the object down. 

F_g has two components and we show these with black vectors.The bigger black vector pointing down represents the weight.

Whenever there is a weight, there is a normal force and we show the normal force with an orange vector.

Notice also the other location of the angle. We are claiming this is the same angle as the one at the bottom right corner.

We will prove this in another lesson.

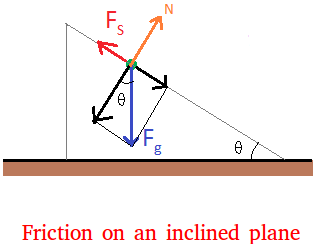
Let's add a few more stuff that will help us to solve the problem.

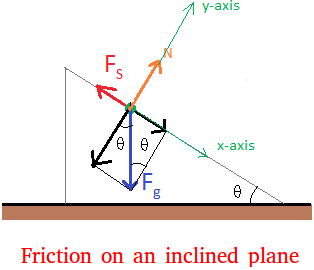
Second important concept when dealing with friction on an inclined plane

Apply Newton's second law:

Newton's second law is F = m × a

F is the sum of all forces.

If we apply Newton's second law along the y-axis, we get:

N - big black vector = m × a

When the object is on the verge of moving, it is not moving, so the acceleration is equal to 0.

The equation becomes

N - big black vector = m × 0

N - big black vector = 0

We can use trigonometric identities to find the big black vector.

By the same fashion,


N - cos θ×F_g = 0

N = cos θ×F_g

If we apply Newton's second along the x-axis, we get:

Small black vector - F_s = 0



sin θ× F_g - F_s = 0

sin θ× F_g = F_s

Now we can use the formula f_{s, max} = μ_s × N


μ_s = tan θ

μ_s = 0.5773

This lesson about friction on an inclined plane is a little challenging.

Make sure you master trigonometric identities, vectors, and normal force before reading this lesson.