Graph of the absolute value of x

The graph of the absolute value of x is called parent absolute value function. The reason it is given this name is because the absolute value of x is the easiest of all absolute value functions to graph.

Using f(x) = |x| we see that, m = 1, b = 0, and c  = 0

You can graph the absolute value of x by looking for the vertex and several other selected points.

First, find the vertex.

The vertex is located at (-b / m , c)

Therefore, the vertex is (-0 / 1, 0) or (0,0)

Now, evaluate the function for several selected values of x.

f(1) = |1| = 1

The point is (1,1)

f(-1) = |-1| = 1

The point is (-1,1)

f(2) = |2| = 2

The point is (2,2)

f(-2) = |-2| = 2

The point is (-2,2)

f(3) = |3| = 3

The point is (3,3)

f(-3) = |-3| = 3

The point is (-3,3)

Now, graph the following 7 points: (0,0), (1,1), (-1,1), (2,2), (-2,2), (3,3), and (-3,3)

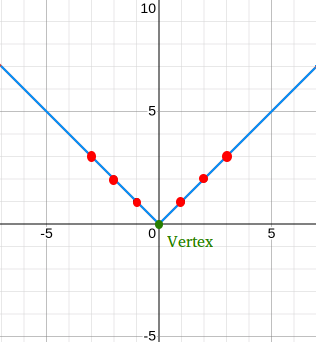
Things to notice about the graph of the absolute value of x

• The angle at the vertex is a right angle.

• The graph is symmetric about the y-axis.

• The linear "piece" on the right side of the y-axis has a slope of 1 and the linear "piece" on the left side of the y-axis has a slope of -1.

• The graph is located on both sides of the y-axis, so the domain is all real numbers or (-∞, ∞)

• The graph is located above the x-axis with the exception of the point (0,0), so the range is all non-negative real numbers or [0, ∞)