Graphing exponential decay

When graphing exponential decay, it is always a good idea to make a table of values and you could look for at least 5 points that you can use to make the graph. In the table below, we use 6 points.

It is also a good idea to choose both negative and positive values for x, especially numbers that are opposites. For example, notice how we chose x = -1 and x = 1.

Graph y = 20 × 0.5^x

x	20×0.5^x	(x, y)
-2	20×0.5^-2 = 20 / 0.5² = 20/0.25 = 20 / (1/4) = 20 × 4 = 80	(-2, 80)
-1	20×0.5^-1 = 20 / 0.5¹ = 20/0.5 = 20 / (1/2) = 20 × 2 = 40	(-1, 40)
0	20×0.5⁰ = 20 × 1 = 20	(0, 20)
1	20×0.5¹ = 20 × 0.5 = 20 × 1/2 = 10	(1, 10)
2	20×0.5² = 20 × 0.25 = 20 × 1/4 = 5	(2, 5)
3	20×0.5³ = 20 × 0.125 = 20 × 1/8 = 2.5	(3, 2.5)

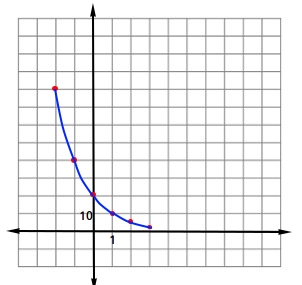
Did you make the following observations about the figure above?

Each square in vertical axis or y-axis represents 10 units.

Each square in horizontal axis or x-axis represents 1 unit.

Important observations when graphing exponential decay

Now, let us see what will happen if we choose the following values for x:

x = -4, -10, -20

If x = -4, y = 20 × 0.5^-4 = 20 / 0.5⁴ = 20 / (1/2)⁴ = 20 / (1/16) = 20×16 = 320.

If x = -10, y = 20 × 0.5^-10 = 20 / 0.5¹⁰ = 20 / (1/2)¹⁰ = 20 / (1/1024) = 20×1024 = 20480.

If x = -20, y = 20 × 0.5^-20 = 20 / 0.5²⁰ = 20 / (1/2)²⁰ = 20 / (1/1048576) = 20×1048576 = 20971520.

When graphing exponential decay, as the values of x get smaller and smaller, the values of y get bigger and bigger. In other words, the values of y will approach infinity.

Now, let us see what will happen if we choose the following values for x:

x = 4, 10, 20

If x = 4, y = 20 × 0.5⁴ = 20 × 0.0625 = 1.25

If x = 10, y = 20 × 0.5¹⁰ = 20 × 0.0009765625 = 0.01953

If x = 20, y = 20 × 0.5²⁰ = 20 × 0.0000009537 = 0.000019074

As x increases, y decreases exponentially or decreases rapidly. The value of y get closer and closer to 0.

Exponential and logarithmic functions

Graphing exponential growth