Four hard order of operations problems

The first two were found online and I made up the last two. 

Problem #1:  

6 ÷2(1 + 2)

This problem was on Facebook and many people got it wrong. According to PEMDAS, The first thing to do is parenthesis.

6 ÷2(1 + 2) =  6 ÷2(3)

Now this is where many people got it wrong. They try to follow PEMDAS by multiplying 2 and 3 to get 6. The problem became  6 ÷ 6 and  6 ÷ 6 = 1

Because the M comes before D, it makes people feel that they have to multiply first.

MD in PEMDAS means to multiply and / or divide from left to right and it does not matter if multiplication is first or not.

The correct way to do it then is to divide 6 by 2 first.

6 ÷2(3) = 3(3) = 9. 

Problem #2:  

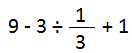
Apparently, many people got it wrong in Japan. What makes this problem hard and tricky? Or is it really?

We need two concepts to solve this problem. First, according to PEMDAS, do division. 
Then, you need to know of course how to do this division.

3 ÷ 1/3 = 3 × 3/1 = 9

After that, everything is easy

9 - 9 + 1 = 0 + 1 = 1

Very hard order of operations problems

Problem #3:

10 × 4 - 2 × (4² ÷ 4) ÷ 2 ÷ 1/2 + 9

= 10 × 4 - 2 × (16 ÷ 4) ÷ 2 ÷ 1/2 + 9

= 10 × 4 - 2 × (4) ÷ 2 ÷ 1/2 + 9

= 10 × 4 - 8 ÷ 2 ÷ 1/2 + 9

= 10 × 4 - 4 ÷ 1/2 + 9

 =10 × 4 -  8 + 9

= 40 - 8 + 9

= 32 + 9

= 41

Problem #4:

-10 ÷ (20 ÷ 2² × 5 ÷ 5) × 8 - 2  

-10 ÷ (20 ÷ 2² × 5 ÷ 5) × 8 - 2  

First stay inside the parenthesis until you get a single number

-10 ÷ (20 ÷ 4 × 5 ÷ 5) × 8 - 2

-10 ÷ (5 × 5 ÷ 5) × 8 - 2    (20 ÷ 4 = 5) 

-10 ÷ (25 ÷ 5) × 8 - 2        (5 × 5 = 25)

Now again, resist the urge to do multiplication first and remember that a negative divided by a positive is a negative.

-10 ÷ (5) × 8 - 2 

-2 × 8 - 2

-16 - 2

-18