Horizontal line test
In mathematics, one can use the horizontal line test in order to determine if a function is one-to-one or injective.
The image below shows what a horizontal line test is supposed to look like.
The green line is the line that we use to do the test. It is basically a horizontal line that can cross or intersect a graph in at least 1 point.
In the image below, the line intersects the graph in two points and these points are (-1,-1) and (2, -1).
Study the image carefully!
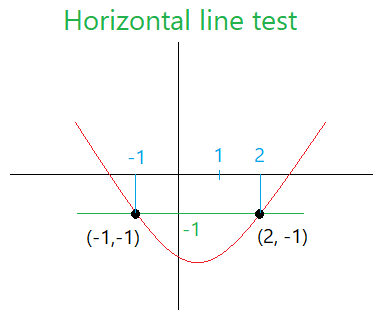
Horizontal line test and one-to-one function
If a horizontal line test intersects the graph in more than one point, then the graph is not one-to-one. Therefore, the graph above is not one-to-one since the line intersects the graph in two points.
See below another horizontal line test that intersects the graph in only 1 point.
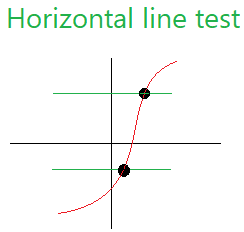
Here we draw two lines to emphasize the fact that no matter how many horizontal lines you draw, they will always cut or intersect this graph in only 1 point.
Since every horizontal line test will always cut the graph in only 1 point, we say that the graph immediately above is one-to-one.
What is the difference between a horizontal line test and a vertical line test?
The first graph we drew above is not one-to-one because the horizontal line crossed the two points (-1,-1) and (2, -1). As you can see here, two different x-values and these are - 1 and 2 are mapped to the same y-value or -1
When you do a horizontal line test, each x-value in the domain should be mapped to a different y-value in the range every time.
Other other hand, when you a vertical line test, each y-value in the range should be mapped to a different x-value in the domain.