Vertical line test

A vertical line test is a visual way to determine if the graph of a relation is a function using a vertical line.

If the vertical line passes through at least two points on the graph, then an element in the domain is paired with more than 1 element in the range. As a result, the relation is not a function.

If on the other hand, the vertical line passes through at the most 1 point, then an element in the domain is paired with only 1 element in the range. The relation is then a function.

The line has to be vertical as illustrated below. You will see a correct vertical line test and an incorrect vertical line test.

Vertical line

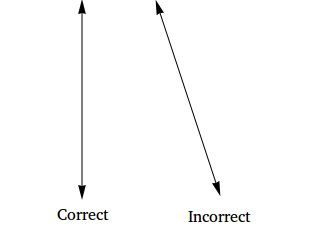
Some examples showing how to use the vertical line test to check if a relation is a function or not.

Next, we show you a few examples where the vertical line test was used to determine if the graph is a function. 

Example #1

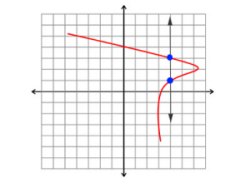Not a functionVertical line test

Notice the two blue points. This means that the vertical line passes through 2 points. 

Can you guess what these two points are just by looking at the graph?

These two points are (4, 1) and (4, 3). As you can see, 4, which is an element in the domain, is paired with two elements in the range. As a result, the relation above is not a function.

Example #2

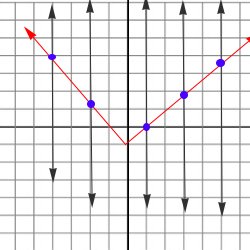Is a functionVertical line test

Here, there are 5 vertical lines and none of them passes through at least 2 points. Therefore, this graph is a function.

Important things to keep in mind:

  • Notice that a vertical line is always going to be parallel to the y-axis.
  • Draw many vertical lines before you draw your conclusion.
  • You are looking for the point(s) of intersection between the vertical line and the graph.

Some examples of relations that are also functions and will always pass the vertical line test. 

y = 3x + 1

y = x3

y = |x|

y = |2x +1|

y = √(x- 2)

y = x4 + x3 + 1

Some examples of relations that are not functions and will never pass the vertical line test. 

x2 + y2 = 4

y2 - 3x = 7

y =  ± √(2 + 5x)

All lines, except a vertical line, will pass a vertical line test. 

Circles and ellipses will never pass the vertical line test.

Parabolas and hyperbolas may or many not pass the vertical line test.

Horizontal line test